Matrix Diffusion

From Enviro Wiki
Jump to: navigation, search

Matrix diffusion occurs when dissolved groundwater contaminants present in zones with greater hydraulic conductivity (K) are transported by molecular diffusion into lower K zones, slowing the rate of contaminant migration in the high K zone. However, once the contaminant source is eliminated, contaminants diffuse back out of low K zones, slowing the cleanup rate in the high K zone. In some cases, matrix diffusion can maintain contaminant concentrations in more permeable zones at greater than target cleanup goals for decades or potentially even centuries after the primary sources have been addressed[1]. Field and laboratory results have illustrated the importance of this process. Analytical and numerical modeling tools are available for evaluating matrix diffusion.

Related Article(s):


Contributor(s): Dr. Charles Newell and Dr. Robert Borden


Key Resource(s):

Introduction

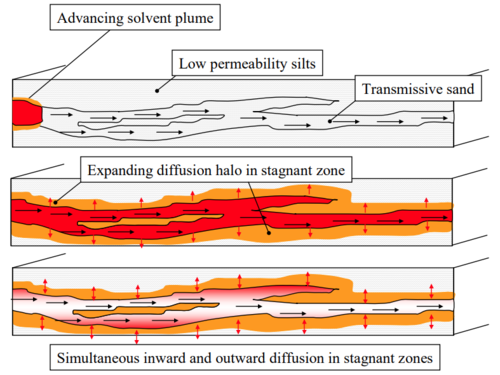
Figure 1. Diffusion of a dissolved solute (chlorinated solvent) into lower K zones during loading period, followed by diffusion back out into higher K zones once the source is removed [3]

Matrix Diffusion can have major impacts on solute migration in groundwater and on cleanup time following source removal. As a groundwater plume advances downgradient, dissolved contaminants are transported by molecular diffusion from zones with larger hydraulic conductivity (K) into lower K zones, slowing the rate of contaminant migration in the high K zone. However, once the contaminant source is eliminated, contaminants diffuse out of low K zones, slowing the cleanup rate in the high K zone (Figure 1). This process, termed ‘back diffusion’, can greatly extend cleanup times.

The impacts of back diffusion on aquifer cleanup have been examined in controlled laboratory experiments by several investigators[4][5][6][7]. The video in Figure 2 shows the results of a 122-day tracer test in a laboratory flow cell (sand tank)[4]. The flow cell contained several clay zones (K = 10-8 cm/s) surrounded by sand (K = 0.02 cm/s). During the loading period, water containing a green fluorescent tracer migrated from left to right with the water flowing through the flow cell, while also diffusing into the clay. After 22 days, the fluorescent tracer is eliminated from the feed, and most of the green tracer is quickly flushed from the tank’s sandy zones. However, small amounts of tracer continue to diffuse out of the clay layers for over 100 days. This illustrates how back diffusion of contaminants out of low K zones can maintain low contaminant concentrations long after the contaminant source as been eliminated.

Figure 2. Video of dye tank simulation of matrix diffusion

In some cases, matrix diffusion can maintain contaminant concentrations in more permeable zones above target cleanup goals for decades or potentially even centuries after the primary sources have been addressed. At a site impacted by Dense Non-Aqueous Phase Liquids (DNAPL), trichloroethene (TCE) concentrations in downgradient wells declined by roughly an order-of-magnitude (OoM) when the upgradient source area was isolated with sheet piling. However, after this initial decline, TCE concentrations appeared to plateau or decline more slowly, consistent with back diffusion from an underlying aquitard. Numerical simulations indicated that back diffusion would cause TCE concentrations in downgradient wells at the site to remain above target cleanup levels for centuries[1].

One other implication of matrix diffusion is that plume migration is attenuated by the loss of contaminants into low permeability zones, leading to slower plume migration compared to a case where no matrix diffusion occurs. This phenomena was observed as far back as 1985 when Sudicky et al. observed that “A second consequence of the solute-storage effect offered by transverse diffusion into low-permeability layers is a rate of migration of the frontal portion of a contaminant in the permeable layers that is less than the groundwater velocity.”[8] In cases where there is an attenuating source, matrix diffusion can also reduce the peak concentrations observed in downgradient monitoring wells. The attenuation caused by matrix diffusion may be particularly important for implementing Monitored Natural Attenuation (MNA) for contaminants that do not completely degrade, such as heavy metals and Perfluoroalkyl and Polyfluoroalkyl Substances (PFAS).

SERPD/ESTCP Research

The SERDP/ESTCP programs have funded several projects focusing on how matrix diffusion can impede progress towards reaching site closure, including:

Transport Modeling

Several different modeling approaches have been developed to simulate the diffusive transport of dissolved solutes into and out of lower K zones[12][13]. The Matrix Diffusion Toolkit[9] is a Microsoft Excel based tool for simulating forward and back diffusion using two different analytical models[14][15]. Numerical models including MODFLOW/MT3DMS[16] have been shown to be effective in simulating back diffusion processes and can accurately predict concentration changes over 3 orders-of-magnitude in heterogeneous sand tank experiments[17]. However, numerical models require a fine vertical discretization with short time steps to accurately simulate back diffusion, greatly increasing computation times[18]. These issues can be addressed by incorporating a local 1-D model domain within a general 3D numerical model[19].

The REMChlor - MD toolkit is capable of simulating matrix diffusion in groundwater contaminant plumes by using a semi-analytical method for estimating mass transfer between high and low permeability zones that provides computationally accurate predictions, with much shorter run times than traditional fine grid numerical models[11].

Impacts on Breakthrough Curves

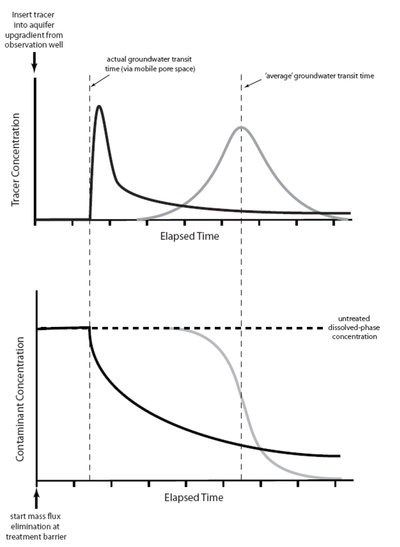
Figure 3. Comparison of tracer breakthrough (upper graph) and cleanup curves (lower graph) from advection-dispersion based (gray lines) and advection-diffusion based (black lines) solute transport[20].

The impacts of matrix diffusion on the initial breakthrough of the solute plume and on later cleanup are illustrated in Figure 3[20]. Using a traditional advection-dispersion model, the breakthrough curve for a pulse tracer injection appears as a bell-shaped (Gaussian) curve (gray line on the right side of the upper graph) where the peak arrival time corresponds to the average groundwater velocity. Using an advection-diffusion approach, the breakthrough curve for a pulse injection is asymmetric (solid black line) with the peak tracer concentration arriving earlier than would be expected based on the average groundwater velocity, but with a long extended tail to the flushout curve.

The lower graph shows the predicted cleanup concentration profiles following complete elimination of a source area. The advection-dispersion model (gray line) predicts a clean-water front arriving at a time corresponding to the average groundwater velocity. The advection-diffusion model (black line) predicts that concentrations will start to decline more rapidly than expected (based on the average groundwater velocity) as clean water rapidly migrates through the highest-permeability strata. However, low but significant contaminant concentrations linger much longer (tailing) due to diffusive contaminant mass exchange between zones of high and low permeability. A similar response to source remediation is seen in models such as the sand tank experiment shown in Figure 2, and also in field observations of plume contaminant concentrations in heterogeneous aquifers.


References

  1. ^ 1.0 1.1 Chapman, S.W. and Parker, B.L., 2005. Plume persistence due to aquitard back diffusion following dense nonaqueous phase liquid source removal or isolation. Water Resources Research, 41(12), Report W12411. DOI: 10.1029/2005WR004224 Report.pdf Free access article from American Geophysical Union
  2. ^ 2.0 2.1 Sale, T., Parker, B.L., Newell, C.J. and Devlin, J.F., 2013. Management of Contaminants Stored in Low Permeability Zones – A State of the Science Review. Strategic Environmental Research and Development Program (SERDP) Project ER-1740. Report.pdf Website: ER-1740
  3. ^ Sale, T.C., Illangasekare, T.H., Zimbron, J., Rodriguez, D., Wilking, B., and Marinelli, F., 2007. AFCEE Source Zone Initiative. Air Force Center for Environmental Excellence, Brooks City-Base, San Antonio, TX. Report.pdf
  4. ^ 4.0 4.1 Doner, L.A., 2008. Tools to resolve water quality benefits of upgradient contaminant flux reduction. Master’s Thesis, Department of Civil and Environmental Engineering, Colorado State University.
  5. ^ Yang, M., Annable, M.D. and Jawitz, J.W., 2015. Back Diffusion from Thin Low Permeability Zones. Environmental Science and Technology, 49(1), pp. 415-422. DOI: 10.1021/es5045634 Free download available from: ResearchGate
  6. ^ Yang, M., Annable, M.D. and Jawitz, J.W., 2016. Solute source depletion control of forward and back diffusion through low-permeability zones. Journal of Contaminant Hydrology, 193, pp. 54-62. DOI: 10.1016/j.jconhyd.2016.09.004 Free download available from: ResearchGate
  7. ^ Tatti, F., Papini, M.P., Sappa, G., Raboni, M., Arjmand, F., and Viotti, P., 2018. Contaminant back-diffusion from low-permeability layers as affected by groundwater velocity: A laboratory investigation by box model and image analysis. Science of The Total Environment, 622, pp. 164-171. DOI: 10.1016/j.scitotenv.2017.11.347
  8. ^ Sudicky, E.A., Gillham, R.W., and Frind, E.O., 1985. Experimental Investigation of Solute Transport in Stratified Porous Media: 1. The Nonreactive Case. Water Resources Research, 21(7), pp. 1035-1041. DOI: 10.1029/WR021i007p01035
  9. ^ 9.0 9.1 Farhat, S.K., Newell, C.J., Seyedabbasi, M.A., McDade, J.M., Mahler, N.T., Sale, T.C., Dandy, D.S. and Wahlberg, J.J., 2012. Matrix Diffusion Toolkit. Environmental Security Technology Certification Program (ESTCP) Project ER-201126. User’s Manual.pdf Website: ER-201126
  10. ^ Sale, T. and Newell, C., 2011. A Guide for Selecting Remedies for Subsurface Releases of Chlorinated Solvents. Environmental Security Technology Certification Program (ESTCP) Project ER-200530. Report.pdf Website: ER-200530
  11. ^ 11.0 11.1 Farhat, S. K., Newell, C. J., Falta, R. W., and Lynch, K., 2018. A Practical Approach for Modeling Matrix Diffusion Effects in REMChlor. Environmental Security Technology Certification Program (ESTCP) Project ER-201426. User’s Manual.pdf Website: ER-201426
  12. ^ Falta, R.W., and Wang, W., 2017. A semi-analytical method for simulating matrix diffusion in numerical transport models. Journal of Contaminant Hydrology, 197, pp. 39-49. DOI: 10.1016/j.jconhyd.2016.12.007
  13. ^ Muskus, N. and Falta, R.W., 2018. Semi-analytical method for matrix diffusion in heterogeneous and fractured systems with parent-daughter reactions. Journal of Contaminant Hydrology, 218, pp. 94-109. DOI: 10.1016/j.jconhyd.2018.10.002
  14. ^ Parker, B.L., Gillham, R.W., and Cherry, J.A., 1994. Diffusive Disappearance of Immiscible Phase Organic Liquids in Fractured Geologic Media. Groundwater, 32(5), pp. 805-820. DOI: 10.1111/j.1745-6584.1994.tb00922.x
  15. ^ Sale, T.C., Zimbron, J.A., and Dandy, D.S., 2008. Effects of reduced contaminant loading on downgradient water quality in an idealized two-layer granular porous media. Journal of Contaminant Hydrology, 102(1), pp. 72-85. DOI: 10.1016/j.jconhyd.2008.08.002
  16. ^ Zheng, C. and Wang, P.P., 1999. MT3DMS: A Modular Three-Dimensional Multispecies Transport Model for Simulation of Advection, Dispersion, and Chemical Reactions of Contaminants in Groundwater Systems; Documentation and User’s Guide. Contract Report SERDP-99-1 U.S. Army Engineer Research and Development Center, Vicksburg, MS. User’s Guide.pdf MT3DMS website
  17. ^ Chapman, S.W., Parker, B.L., Sale, T.C., Doner, L.A., 2012. Testing high resolution numerical models for analysis of contaminant storage and release from low permeability zones. Journal of Contaminant Hydrology, 136, pp. 106-116. DOI: 10.1016/j.jconhyd.2012.04.006
  18. ^ Farhat, S.K., Adamson, D.T., Gavaskar, A.R., Lee, S.A., Falta, R.W. and Newell, C.J., 2020. Vertical Discretization Impact in Numerical Modeling of Matrix Diffusion in Contaminated Groundwater. Groundwater Monitoring and Remediation, 40(2), pp. 52-64. DOI: 10.1111/gwmr.12373
  19. ^ Carey, G.R., Chapman, S.W., Parker, B.L. and McGregor, R., 2015. Application of an Adapted Version of MT3DMS for Modeling Back‐Diffusion Remediation Timeframes. Remediation, 25(4), pp. 55-79. DOI: 10.1002/rem.21440
  20. ^ 20.0 20.1 Interstate Technology and Regulatory Council (ITRC), 2011. Integrated DNAPL Site Strategy (IDSS-1), Integrated DNAPL Site Strategy Team, ITRC, Washington, DC. Report.pdf Free download from: ITRC

See Also

Retrieved from "https://www.enviro.wiki/index.php?title=Matrix_Diffusion&oldid=15806"