Plume Response Modeling
Plume response modeling simulates how groundwater contaminant plumes respond to contaminant source control. Understanding the plume response is important because plumes may grow, stabilize, or shrink depending on the source strength and history, and the plume attenuation mechanisms. Plume response modeling can be used to help evaluate source and plume remediation strategies.
Related Article(s):
Contributor(s): Dr. Ron Falta
Key Resource(s):
- Methodology for comparing source and plume remediation alternatives[1]
- REMChlor remediation evaluation model for chlorinated solvents user’s manual[2]
- Modeling remediation of chlorinated solvent plumes[3]
Introduction
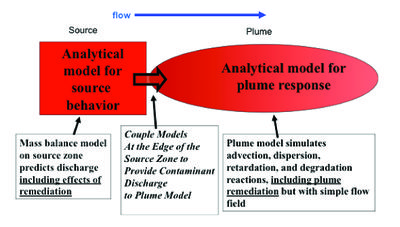
Plume models simulate advection, dispersion, retardation, and reactions of contaminants as they migrate downgradient from the source zone. As source zones undergo remediation or natural attenuation, the contaminant loading to the plumes decreases with time. The decreased loading may or may not result in stabilization or shrinkage of the plume, which is also affected by the plume remediation including natural attenuation. Modeling plume response to remediation, therefore, must consider the nature and timing of both the source and the plume remediation. Ideally, this would be done in a single model, but it is usually done by combining source zone and plume response models. Here, we discuss the plume response models.
Analytical Plume Models
Analytical plume models simulate contaminant transport assuming a simple uniform groundwater flow field. Despite this simplifying assumption, analytical models are widely used at contaminated sites, particularly for initial screening level calculations. Examples of analytical plume models include:
The REMChlor model employs an analytical mass balance source function that accounts for partial or complete source remediation at any time. A time-dependent source model is coupled to the plume model (Fig. 1).
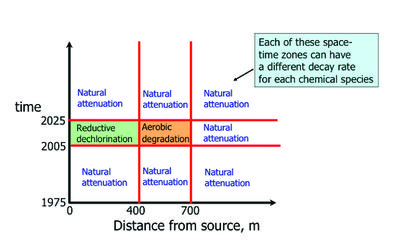
REMChlor allows for spatially and temporally variable contaminant decay rates in the plume. These decay rates can be user manipulated to simulate plume remediation activities or natural attenuation. Figure 2 shows an example of a plume remediation scheme that could be simulated in REMChlor.
Plume response to remediation depends on characteristics of both the source and the plume behavior. Some plumes may persist long after source remediation, while others may attenuate without any source or plume remediation.
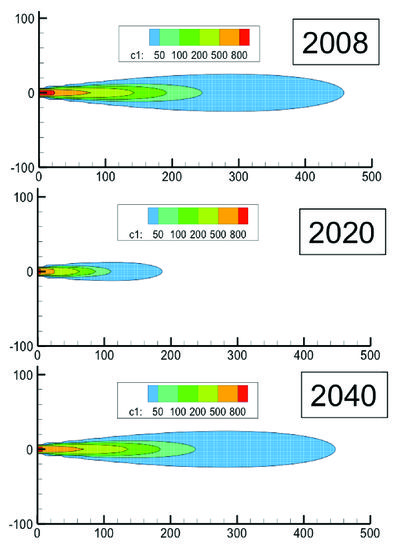
The following REMChlor modeling example illustrates one type of plume behavior than can occur with a persistent dense non-aqueous phase liquids (DNAPL) source (from Falta and Kueper 2014[6]). In this example, it is assumed that 200 kg of 1,2-DCA was released into a aquifer in 1980. The groundwater pore velocity (the Darcy velocity divided by soil porosity, sometimes called groundwater seepage velocity) is 60 m/yr, the initial source concentration is 1 mg/L, the retardation factor is 2, and the natural attenuation decay rate in the plume corresponds to a half-life of 2 years. The time-dependent source concentration is assumed to be a linear function of the source mass. The top panel in Figure 3 shows the dissolved 1,2-DCA plume in 2008, 28 years after the initial release.
Enhanced plume remediation was simulated between 2010 and 2020 by increasing the 1,2-DCA decay rate over the first 300 m to correspond to a half-life of 0.5 year. This remediation has the effect of greatly shrinking the plume (2020 panel, Fig. 3), but the plume almost completely rebounds after the plume treatment ends (2040 panel, Fig. 3). The plume rebound in this case was due to the fact that the 1,2-DCA source strength remains high due to the low rate of source depletion in this scenario.
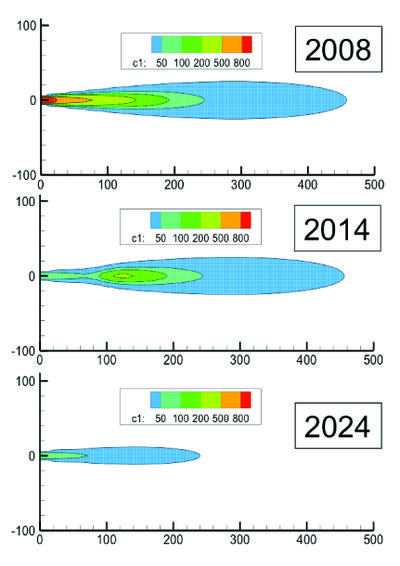
Source remediation was modeled by removing 90% of the source mass that remained in 2010 (Fig. 4). The source remediation causes part of the plume to become isolated from the source due to the reduced source strength (2014 panel, Fig. 4). Eventually, the effect of source remediation is felt throughout the plume, and the plume stabilizes at a much smaller size (2024 panel, Fig. 4). The plume in this example does not completely attenuate because it was assumed that the source remediation effort was not perfect, leaving behind 10% of the mass in the source zone.
Numerical Plume Models
Numerical plume models solve the groundwater flow and contaminant transport equations. These two processes are typically decoupled, and solved separately. A good example of such a decoupled flow and transport model is the MODFLOW[7] and MT3DMS[8] combination. A groundwater transport simulation is performed by first calculating the transient or steady-state groundwater flow field using MODFLOW. Then the MT3DMS transport simulation is run using the flow field from MODFLOW. This approach works well as long as the contaminant transport does not affect the flow field. For problems where contaminant concentrations cause buoyancy effects (e.g., salt water intrusion), the equations must be coupled together and solved simultaneously. Other widely used plume models include:
Numerical plume models may be used with either a numerical or an analytical source zone model. The coupling of a numerical flow and transport model with a numerical source zone model is fairly complex, and has been done mainly in a research setting (e.g., [12][13][14][15][16]). More typically, numerical plume models are run in one of two ways: 1) a constant source term is assumed where concentration does not change over time; or 2) the a simpler analytical source model is run outside of the numerical model and source concentration vs. time data over many years are then entered into the numerical model to simulate source attenuation[3]. One new modeling tool is the MODFLOW-USG groundwater flow model, where USG stands for “unstructured grids”[17][18]. Unstructured grids allow for inclusion of various cell geometries and grid-nesting methodologies to provide finer resolution of complex stratigraphy and other hydrologic features. This model is emerging as the standard for modeling groundwater flow, and can be used with the MODPATH Version 7[19] to simulate groundwater plumes using particle tracking. A solute transport model, USG-Transport, is currently being beta tested on the Groundwater Vistas platform in 2016.
Matrix Diffusion in Plumes
There is a growing consensus that molecular diffusion of contaminants into and out of low permeability zones can play a significant and even dominant role in plume response. Matrix diffusion, also called “back diffusion,” occurs when contaminants such as chlorinated solvents diffuse from high permeability zones into adjacent low permeability zones during a “loading period.” During the “release period,” the contamination may be removed from the high permeability zones, but contaminants in the low permeability zones gradually diffuse back into the high permeability zones at significant levels[20][21][22][23][24][25][26][27][28][29][12][30][31][32]. This process may occur in any heterogeneous setting, but it is particularly important in certain fractured bedrock sites, and in sites with extensive clay lenses or layers. These types of complex site conditions tend to lead to plumes that are long lived, requiring extensive long-term monitoring. Matrix diffusion is explained in a 2013 SERDP Report[33]. Both numerical and analytical modeling approaches have been used to simulate matrix diffusion. Examples of the numerical approach can be found in Chapman and Parker (2005)[30], Chapman et al. (2012)[34], and Chapman and Parker (2013)[35]. These publications describe high-resolution 2D simulations that capture the plume matrix diffusion process. But a key constraint with using numerical models to simulate matrix diffusion is that very high resolution modeling grids or mesh networks are required. For example, Chapman and Parker (2012)[34] used 9,000 cells in MT3D to simulate matrix diffusion in a small-scale research tank experiment 1.1 meters long and 0.84 meters high. In practice, conventional numerical transport models may need many thin layers just a few centimeters thick to accurately simulate plumes affected by matrix diffusion (e.g., see Rasa et al., (2011)[36]). Analytical models for matrix diffusion include the:
The parallel fracture models consider advection, dispersion, retardation, and decay in the fracture, with diffusion, retardation, and decay in the matrix. The two-layer model by Sale et al. (2008)[32] considers advection, dispersion, retardation and decay in the aquifer with diffusion, retardation, and decay in an underlying aquitard. Finally, the Sale et al. (2008)[32] and Seyedabbasi et al. (2012)[39] models are included in the ESTCP Matrix Diffusion Toolkit[40]. An enhanced version of the REMChlor model with a matrix diffusion term in the plume (it could already represent matrix diffusion in the source using the gamma source term) called REMChlor-MD is now available.
Summary
Plume response to source remediation can be simulated using analytical or numerical approaches. Analytical models are easy to set up and run, but they assume simplified flow conditions that may not be realistic at some sites. These models are most appropriate for screening-level calculations and for simple sites. Numerical models take more effort to set up and run, but they have the flexibility to simulate complicated flow fields, and transient flow effects such as groundwater pumping. However, most numerical models do not simulate source attenuation directly and other models are needed to simulate plume response to changes in the source over time. Matrix diffusion may play a significant role at some sites, and newer analytical and numerical approaches are available for simulating this mechanism in plume response modeling.
References
- ^ 1.0 1.1 1.2 Falta, R.W., 2008. Methodology for comparing source and plume remediation alternatives. Ground Water, 46(2), 272-285. doi: 10.1111/j.1745-6584.2007.00416.x
- ^ 2.0 2.1 Falta, R.W., Stacy, M.B., Ahsanuzzaman, A.N.M., Wang, M. and Earle, R., 2007. REMChlor remediation evaluation model for chlorinated solvents user’s manual Version 1.0. Cent. for subsurface model. support, US Environ. Prot. Agency, Ada, Okla. User's Manual v1.0
- ^ 3.0 3.1 Rifai, H.S., Borden, R.C., Newell, C.J. and Bedient, P.B., 2010. Modeling remediation of chlorinated solvent plumes. In In Situ Remediation of Chlorinated Solvent Plumes, pgs. 145-184. Springer, New York. doi: 10.1007/978-1-4419-1401-9_6
- ^ Aziz, C.E., Smith, A.P., Newell, C.J. and Gonzales, J.R., 2000. BIOCHLOR Chlorinated solvent plume database report. Air Force Center for Environmental Excellence, Texas. Report pdf
- ^ Aziz, C.E., Newell, C.J. and Gonzales, J.R., 2002. BIOCHLOR natural attenuation decision support system version 2.2 user’s manual addendum. Groundwater Services, Inc., Houston, Texas for the Air Force Center for Environmental Excellence. Report pdf
- ^ 6.0 6.1 6.2 Falta, R.W. and Kueper, B.H., 2014. Modeling plume responses to source treatment. In Chlorinated Solvent Source Zone Remediation, pgs. 145-186. Springer, New York. doi: 10.1007/978-1-4614-6922-3_6
- ^ McDonald, M.G. and Harbaugh, A.W., 1988. A modular three-dimensional finite-difference ground-water flow model. U.S. Geological Survey, Techniques of Water-Resources Investigations, Book 6, Modeling Techniques.
- ^ Zheng, C. and Wang, P.P., 1999. MT3DMS: a modular three-dimensional multispecies transport model for simulation of advection, dispersion, and chemical reactions of contaminants in groundwater systems; documentation and user's guide. Contract Report SERDP-99-1 U.S. Army Engineer Research and Development Center, Vicksburg, MS. Report pdf
- ^ Clement, T.P., 1997. A modular computer code for simulating reactive multi-species transport in 3-dimensional groundwater systems. Pacific Northwest National Laboratory, 11720. Report pdf
- ^ Widdowson, M.A., Waddill, D.W. and Ruiz, C.E., 1997. SEAM3D: A numerical model for three-dimensional solute transport and sequential electron acceptor-based bioremediation in groundwater. In Groundwater: An Endangered Resource, pgs. 83-88. ASCE.
- ^ DHI-WASY, 2012. FEFLOW 6.1 Finite element subsurface flow and transport simulation system user manual.
- ^ 12.0 12.1 Parker, J.C. and Park, E., 2004. Modeling field‐scale dense nonaqueous phase liquid dissolution kinetics in heterogeneous aquifers. Water Resources Research, 40(5). doi: 10.1029/2003WR002807
- ^ Zhu, J. and Sykes, J.F., 2004. Simple screening models of NAPL dissolution in the subsurface. Journal of Contaminant Hydrology, 72(1), 245-258. doi: 10.1016/j.jconhyd.2003.11.002
- ^ Grant, G.P. and Gerhard, J.I., 2007. Simulating the dissolution of a complex dense nonaqueous phase liquid source zone: 2. Experimental validation of an interfacial area–based mass transfer model. Water Resources Research, 43(12). doi: 10.1029/2007WR006039
- ^ Christ, J.A., Ramsburg, C.A., Pennell, K.D. and Abriola, L.M., 2010. Predicting DNAPL mass discharge from pool-dominated source zones. Journal of Contaminant Hydrology, 114(1), 18-34. doi: 10.1016/j.jconhyd.2010.02.005
- ^ West, M.R., Grant, G.P., Gerhard, J.I. and Kueper, B.H., 2008. The influence of precipitate formation on the chemical oxidation of TCE DNAPL with potassium permanganate. Advances in Water Resources, 31(2), 324-338. doi: 10.1016/j.advwatres.2007.08.011
- ^ Panday, Sorab, Langevin, C.D., Niswonger, R.G., Ibaraki, Motomu, and Hughes, J.D., 2013. MODFLOW-USG version 1: An unstructured grid version of MODFLOW for simulating groundwater flow and tightly coupled processes using a control volume finite-difference formulation: U.S. Geological Survey Techniques and Methods, book 6, chap. A45, 66 pgs. USGS MODFLOW-USG version 1 Website
- ^ USGS, 2016. MODFLOW-USG: An unstructured grid version of MODFLOW for simulating groundwater flow and tightly coupled processes using a control volume finite-difference formulation. USGS MODFLOW-USG Website
- ^ USGS, 2016. User guide for MODPATH Version 7-A particle-tracking model for MODFLOW. USGS MODPATH Website
- ^ Parker, B.L., Gillham, R.W. and Cherry, J.A., 1994. Diffusive disappearance of immiscible‐phase organic liquids in fractured geologic media. Ground Water, 32(5), 805-820. doi: 10.1111/j.1745-6584.1994.tb00922.x
- ^ Parker, B.L., McWhorter, D.B. and Cherry, J.A., 1997. Diffusive loss of non‐aqueous phase organic solvents from idealized fracture networks in geologic media. Ground Water, 35(6), 1077-1088. doi: 10.1111/j.1745-6584.1997.tb00180.x
- ^ Ross, B. and Lu, N., 1999. Dynamics of DNAPL penetration into fractured porous media. Ground Water, 37(1), 140-147. doi: 10.1111/j.1745-6584.1999.tb00967.x
- ^ Esposito, S.J. and Thomson, N.R., 1999. Two-phase flow and transport in a single fracture-porous medium system. Journal of Contaminant Hydrology, 37(3), 319-341. doi: 10.1016/S0169-7722(98)00169-7
- ^ Lipson, D.S., Kueper, B.H. and Gefell, M.J., 2005. Matrix Diffusion‐Derived Plume Attenuation in Fractured Bedrock. Ground Water, 43(1), 30-39. doi: 10.1111/j.1745-6584.2005.tb02283.x
- ^ O'Hara, S.K., Parker, B.L., Jorgensen, P.R. and Cherry, J.A., 2000. Trichloroethene DNAPL flow and mass distribution in naturally fractured clay: Evidence of aperture variability. Water Resources Research, 36(1), 135-147. doi: 10.1029/1999WR900212
- ^ Reynolds, D.A. and Kueper, B.H., 2001. Multiphase flow and transport in fractured clay/sand sequences. Journal of Contaminant Hydrology, 51(1), 41-62. doi: 10.1016/S0169-7722(01)00121-8
- ^ Reynolds, D.A. and Kueper, B.H., 2002. Numerical examination of the factors controlling DNAPL migration through a single fracture. Ground Water, 40(4), 368-377. doi:10.1111/j.1745-6584.2002.tb02515.x
- ^ Reynolds, D.A. and Kueper, B.H., 2004. Multiphase flow and transport through fractured heterogeneous porous media. Journal of Contaminant Hydrology, 71(1), 89-110. doi: 10.1016/j.jconhyd.2003.09.008
- ^ Liu, C. and Ball, W.P., 2002. Back diffusion of chlorinated solvent contaminants from a natural aquitard to a remediated aquifer under well‐controlled field conditions: Predictions and measurements. Ground Water, 40(2), 175-184. doi: 10.1111/j.1745-6584.2002.tb02502.x
- ^ 30.0 30.1 Chapman, S.W. and Parker, B.L., 2005. Plume persistence due to aquitard back diffusion following dense nonaqueous phase liquid source removal or isolation. Water Resources Research, 41(12). doi:10.1029/2005WR004224
- ^ Parker, B.L., Chapman, S.W. and Guilbeault, M.A., 2008. Plume persistence caused by back diffusion from thin clay layers in a sand aquifer following TCE source-zone hydraulic isolation. Journal of Contaminant Hydrology, 102(1), 86-104. doi: 10.1016/j.jconhyd.2008.07.003
- ^ 32.0 32.1 32.2 32.3 Sale, T.C., Zimbron, J.A. and Dandy, D.S., 2008. Effects of reduced contaminant loading on downgradient water quality in an idealized two-layer granular porous media. Journal of Contaminant Hydrology, 102(1), 72-85. doi: 10.1016/j.jconhyd.2008.08.002
- ^ Sale, T., Parker, B.L., Newell, C.J. and Devlin, J.F., 2013. Management of Contaminants Stored in Low Permeability Zones-A State of the Science Review. ER-1740. Environmental Security Technology Certification Program (ESTCP) by Colorado State University Fort Collins Department of Civil and Environmental Engineering. ER-1740
- ^ 34.0 34.1 Chapman, S.W., Parker, B.L., Sale, T.C. and Doner, L.A., 2012. Testing high resolution numerical models for analysis of contaminant storage and release from low permeability zones. Journal of Contaminant Hydrology, 136, 106-116. doi: 10.1016/j.jconhyd.2012.04.006
- ^ Chapman, SW and. Parker, B.L., 2013. Chapter 5: Type site simulations, in Sale, T., B.L. Parker, C.J. Newell, and J.F. Devlin, Management of contaminants stored in low permeability zones, SERDP Project ER-1740, 348 p. ER-1740
- ^ Rasa, E., Chapman, S.W., Bekins, B.A., Fogg, G.E., Scow, K.M. and Mackay, D.M., 2011. Role of back diffusion and biodegradation reactions in sustaining an MTBE/TBA plume in alluvial media. Journal of Contaminant Hydrology, 126(3), 235-247. doi: 10.1016/j.jconhyd.2011.08.006
- ^ Sudicky, E.A. and Frind, E.O., 1982. Contaminant transport in fractured porous media: Analytical solutions for a system of parallel fractures. Water Resources Research, 18(6), 1634-1642. doi: 10.1029/WR018i006p01634
- ^ West, M.R., Kueper, B.H. and Novakowski, K.S., 2004. Semi-analytical solutions for solute transport in fractured porous media using a strip source of finite width. Advances in Water Resources, 27(11), 1045-1059. doi: 10.1016/j.advwatres.2004.08.011
- ^ 39.0 39.1 Seyedabbasi, M.A., Newell, C.J., Adamson, D.T. and Sale, T.C., 2012. Relative contribution of DNAPL dissolution and matrix diffusion to the long-term persistence of chlorinated solvent source zones. Journal of Contaminant Hydrology, 134, 69-81. doi: 10.1016/j.jconhyd.2012.03.010
- ^ Farhat, S.K., Newell, C.J., Seyedabbasi, M.A., McDade, J.M., Mahler, N.T., Sale, T.C., Dandy, D.S. and Wahlberg, J.J., 2012. Matrix Diffusion Toolkit. ER-201126. Environmental Security Technology Certification Program (ESTCP) by GSI Environmental Inc., Houston, Texas. ER-201126