Difference between revisions of "Dispersion and Diffusion"

From Enviro Wiki
Jump to: navigation, search
(→‎Macrodispersion)
(→‎Macrodispersion)
Line 119: Line 119:
 
Spatial variations in hydraulic conductivity can increase the apparent spreading of solute plumes observed in groundwater monitoring wells. For example, in an aquifer composed of alternating layers of lower hydraulic conductivity (''K'') silty sand and higher ''K'' sandy gravel layers, the dissolved solute rapidly migrates downgradient through the sandy gravel layers resulting in relatively high concentration fingers surrounded by relatively uncontaminated material. Over time, contaminants in lower ''K'' layers eventually breakthrough at the monitoring well, causing a more gradual further increase in measured concentrations.  This rapid breakthrough followed by gradual increases in solute concentrations gives the appearance of a plume with a very large dispersion coefficient. This spreading of the solute caused by large-scale heterogeneities in the aquifer and the associated spatial variations in advective transport velocity is referred to as macrodispersion.   
 
Spatial variations in hydraulic conductivity can increase the apparent spreading of solute plumes observed in groundwater monitoring wells. For example, in an aquifer composed of alternating layers of lower hydraulic conductivity (''K'') silty sand and higher ''K'' sandy gravel layers, the dissolved solute rapidly migrates downgradient through the sandy gravel layers resulting in relatively high concentration fingers surrounded by relatively uncontaminated material. Over time, contaminants in lower ''K'' layers eventually breakthrough at the monitoring well, causing a more gradual further increase in measured concentrations.  This rapid breakthrough followed by gradual increases in solute concentrations gives the appearance of a plume with a very large dispersion coefficient. This spreading of the solute caused by large-scale heterogeneities in the aquifer and the associated spatial variations in advective transport velocity is referred to as macrodispersion.   
  
−
In some groundwater modeling projects, large values of the dispersion coefficient are used as an adjustment factor to better represent the observed large-scale spreading of plumes<ref name="ITRC2011"/>. Theoretical studies suggest that macrodispersivity will increase with distance near the source, and then increase more slowly farther downgradient, eventually approaching an asymptotic value<ref name="Gelhar1979">Gelhar, L.W., Gutjahr, A.L. and Naff, R.L., 1979. Stochastic analysis of macrodispersion in a stratified aquifer. Water Resources Research, 15(6), pp.1387-1397.  [https://doi.org/10.1029/WR015i006p01387 DOI:10.1029/WR015i006p01387]</ref><ref name="Gelhar1983">Gelhar, L.W. and Axness, C.L., 1983. Three‐dimensional stochastic analysis of macrodispersion in aquifers. Water Resources Research, 19(1), pp.161-180.  [https://doi.org/10.1029/WR019i001p00161 DOI:10.1029/WR019i001p00161]</ref><ref name="Dagan1988">Dagan, G., 1988. Time‐dependent macrodispersion for solute transport in anisotropic heterogeneous aquifers. Water Resources Research, 24(9), pp.1491-1500.  [https://doi.org/10.1029/WR024i009p01491 DOI:10.1029/WR024i009p01491]</ref>.  Figure 2 shows values of macrodispersivity calculated using the theory of Dagan<ref name="Dagan1988"/> with an autocorrelation length of 3 m and several different values of the variance of ''Y'' (σ<small><sup>2</sup><sub>''Y''</sub></small>) where ''Y'' = Log ''K''. The calculated macrodispersivity increases more rapidly and approaches higher asymptotic values for more heterogeneous aquifers with greater variations in ''K'' (larger σ<small><sup>2</sup><sub>''Y''</sub></small>).  The maximum predicted dispersivity values were in the range of 0.5 to 5 m.  Zech, et al. (2015) presented moderate and high reliability measurements of longitudinal macrodispersivity versus distance. Typical values of the longitudinal macrodispersivity varied from 0.1 to 10 m, with much lower values for transverse and vertical dispersivities.  
+
In some groundwater modeling projects, large values of the dispersion coefficient are used as an adjustment factor to better represent the observed large-scale spreading of plumes<ref name="ITRC2011"/>. Theoretical studies suggest that macrodispersivity will increase with distance near the source, and then increase more slowly farther downgradient, eventually approaching an asymptotic value<ref name="Gelhar1979">Gelhar, L.W., Gutjahr, A.L. and Naff, R.L., 1979. Stochastic analysis of macrodispersion in a stratified aquifer. Water Resources Research, 15(6), pp.1387-1397.  [https://doi.org/10.1029/WR015i006p01387 DOI:10.1029/WR015i006p01387]</ref><ref name="Gelhar1983">Gelhar, L.W. and Axness, C.L., 1983. Three‐dimensional stochastic analysis of macrodispersion in aquifers. Water Resources Research, 19(1), pp.161-180.  [https://doi.org/10.1029/WR019i001p00161 DOI:10.1029/WR019i001p00161]</ref><ref name="Dagan1988">Dagan, G., 1988. Time‐dependent macrodispersion for solute transport in anisotropic heterogeneous aquifers. Water Resources Research, 24(9), pp.1491-1500.  [https://doi.org/10.1029/WR024i009p01491 DOI:10.1029/WR024i009p01491]</ref>.  Figure 2 shows values of macrodispersivity calculated using the theory of Dagan<ref name="Dagan1988"/> with an autocorrelation length of 3 m and several different values of the variance of ''Y'' (σ<small><sup>2</sup><sub>''Y''</sub></small>) where ''Y'' = Log ''K''. The calculated macrodispersivity increases more rapidly and approaches higher asymptotic values for more heterogeneous aquifers with greater variations in ''K'' (larger σ<small><sup>2</sup><sub>''Y''</sub></small>).  The maximum predicted dispersivity values were in the range of 0.5 to 5 m.  Zech, et al. (2015)<ref>Zech, A., Attinger, S., Cvetkovic, V., Dagan, G., Dietrich, P., Fiori, A., Rubin, Y. and Teutsch, G., 2015. Is unique scaling of aquifer macrodispersivity supported by field data? Water Resources Research, 51(9), pp.7662-7679.  [https://doi.org/10.1002/2015WR017220 DOI: 10.1002/2015WR017220]&nbsp;&nbsp; Free access article from [https://agupubs.onlinelibrary.wiley.com/doi/epdf/10.1002/2015WR017220 American Geophysical Union]</ref> presented moderate and high reliability measurements of longitudinal macrodispersivity versus distance. Typical values of the longitudinal macrodispersivity varied from 0.1 to 10 m, with much lower values for transverse and vertical dispersivities.  
  
 
===Matrix Diffusion===
 
===Matrix Diffusion===

Revision as of 17:59, 21 December 2020

Dispersion of solutes in flowing groundwater results in the spreading of a contaminant plume from highly concentrated areas to less concentrated areas. In many groundwater transport models, solute transport is described by the advection-dispersion-reaction equation. The dispersion coefficient in this equation is the sum of the molecular diffusion coefficient, the mechanical dispersion coefficient and the macrodispersion effect.

Related Article(s):

CONTRIBUTOR(S): Dr. Charles Newell and Dr. Robert Borden

Key Resource(s):

Molecular Diffusion

Figure 1. Conceptual depiction of diffusion of a dissolved chemical recently placed in a container at Time 1 (left panel) and then distributed throughout the container (right panel) at Time 2.
Figure 2. Conceptual depiction of mechanical dispersion (adapted from ITRC (2011)[3]).

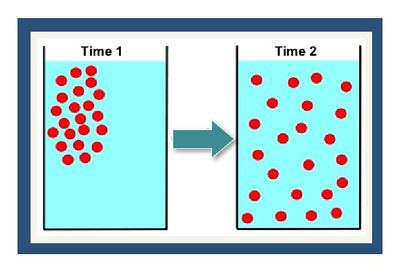
Molecular diffusion is the result of the thermal motion of individual molecules which causes a flux of dissolved solutes from areas of higher concentration to areas of lower concentration (Figure 1). The diffusion coefficient is a proportionality constant between the molar flux due to molecular diffusion and the concentration gradient and is a function of the temperature and molecular weight. In locations where advective flux is low (clayey aquitards and sedimentary rock), diffusion is often the dominant transport mechanism.

The diffusive flux J (M/L2/T) in groundwater is calculated using Fick’s Law:

Equation 1: 
 J = -De dC/dx
Where:
De
 is the effective diffusion coefficient and
dC/dx
 is the concentration gradient.

The effective diffusion coefficient for transport through the porous media, De, is estimated as:

Equation 2: 
 De = Dm ne δ/Τ
Where:
Dm
 is the diffusion coefficient of the solute in water,
ne
 is the effective porosity (dimensionless),
δ
 is the constrictivity (dimensionless) which reflects the restricted motion of particles in narrow pores[4], and
Τ
 is the tortuosity (dimensionless) which reflects the longer diffusion path in porous media around sediment particles[5].

Dm is a function of the temperature, fluid viscosity and molecular weight. Values of Dm for common groundwater solutes are shown in Table 1.

Table 1. Diffusion Coefficients (Dm) for Common Groundwater Solutes.
Aqueous Diffusion Coefficient Temperature
(°C) 		Dm
(cm2/s) 		Reference
Acetone 25   1.16x10-5   Cussler 1997
Benzene 20 1.02x10-5 Bonoli and Witherspoon 1968
Carbon dioxide 25 1.92x10-5 Cussler 1997
Carbon tetrachloride 25 9.55x10-6 Yaws 1995
Chloroform 25 1.08x10-5 Yaws 1995
Dichloroethene 25 1.12x10-5 Yaws 1995
1,4-Dioxane 25 1.02x10-5 Yaws 1995
Ethane 25 1.52x10-5 Witherspoon and Saraf 1965
Ethylbenzene 20 8.10x10-6 Bonoli and Witherspoon 1968
Ethene 25 1.87x10-5 Cussler 1997
Helium 25 6.28x10-5 Cussler 1997
Hydrogen 25 4.50x10-5 Cussler 1997
Methane 25 1.88x10-5 Witherspoon and Saraf 1965
Nitrogen 25 1.88x10-5 Cussler 1997
Oxygen 25 2.10x10-5 Cussler 1997
Perfluorooctanoic acid (PFOA) 20 4.80x10-6 Schaefer et al. 2019
Perfluorooctane sulfonic acid (PFOS) 20 5.40x10-6 Schaefer et al. 2019
Tetrachloroethene 25 8.99x10-6 Yaws 1995
Toluene 20 8.50x10-6 Bonoli and Witherspoon 1968
Trichloroethene 25 8.16x10-6 Rossi et al. 2015
Vinyl chloride 25 1.34x10-5 Yaws 1995

Mechanical Dispersion

Mechanical dispersion (hydrodynamic dispersion) results from groundwater moving at rates both greater and less than the average linear velocity. This is due to: 1) fluids moving faster through the center of the pores than along the edges, 2) fluids traveling shorter pathways and/or splitting or branching to the sides, and 3) fluids traveling faster through larger pores than through smaller pores[6]. Because the invading solute-containing water does not travel at the same velocity everywhere, mixing occurs along flow paths. This mixing is called mechanical dispersion and results in distribution of the solute at the advancing edge of flow. The mixing that occurs in the direction of flow is called longitudinal dispersion. Spreading normal to the direction of flow from splitting and branching out to the sides is called transverse dispersion (Figure 2).

Macrodispersion

Figure 3. Matrix diffusion processes and their effects on plume persistence and attenuation.

Spatial variations in hydraulic conductivity can increase the apparent spreading of solute plumes observed in groundwater monitoring wells. For example, in an aquifer composed of alternating layers of lower hydraulic conductivity (K) silty sand and higher K sandy gravel layers, the dissolved solute rapidly migrates downgradient through the sandy gravel layers resulting in relatively high concentration fingers surrounded by relatively uncontaminated material. Over time, contaminants in lower K layers eventually breakthrough at the monitoring well, causing a more gradual further increase in measured concentrations. This rapid breakthrough followed by gradual increases in solute concentrations gives the appearance of a plume with a very large dispersion coefficient. This spreading of the solute caused by large-scale heterogeneities in the aquifer and the associated spatial variations in advective transport velocity is referred to as macrodispersion.

In some groundwater modeling projects, large values of the dispersion coefficient are used as an adjustment factor to better represent the observed large-scale spreading of plumes[3]. Theoretical studies suggest that macrodispersivity will increase with distance near the source, and then increase more slowly farther downgradient, eventually approaching an asymptotic value[7][8][9]. Figure 2 shows values of macrodispersivity calculated using the theory of Dagan[9] with an autocorrelation length of 3 m and several different values of the variance of Y (σ2Y) where Y = Log K. The calculated macrodispersivity increases more rapidly and approaches higher asymptotic values for more heterogeneous aquifers with greater variations in K (larger σ2Y). The maximum predicted dispersivity values were in the range of 0.5 to 5 m. Zech, et al. (2015)[10] presented moderate and high reliability measurements of longitudinal macrodispersivity versus distance. Typical values of the longitudinal macrodispersivity varied from 0.1 to 10 m, with much lower values for transverse and vertical dispersivities.

Matrix Diffusion

Recently, an alternate conceptual model for describing large-scale plume spreading in heterogeneous soils has been proposed[3][11][12]. In this approach, solute transport in the transmissive zones is reasonably well described by the advection-dispersion equation using relatively small dispersion coefficients representing mechanical dispersion. However, overtime, molecular diffusion slowly transports solutes into lower permeability zones (Figure 3). As the transmissive zones are remediated, these solutes slowly diffuse back out, causing a long extended tail to the flushout curve. This process, referred to as matrix diffusion, is controlled by molecular diffusion and the presence of geologic heterogeneity with sharp contrasts between transmissive and low permeability media[13] as discussed in the video shown in Figure 3.

References

  1. ^ Freeze, A., and Cherry, J., 1979. Groundwater, Prentice-Hall, Englewood Cliffs, New Jersey, 604 pages. Free download from Hydrogeologists Without Borders.
  2. ^ Woessner, W.W., and Poeter, E.P., 2020. Properties of Earth Materials and Principals of Groundwater Flow, The Groundwater Project, Guelph, Ontario, 207 pages. Free download from The Groundwater Project.
  3. ^ 3.0 3.1 3.2 ITRC Integrated DNAPL Site Strategy Team, 2011. Integrated DNAPL Site Strategy. Technical/Regulatory Guidance Document, 209 pgs. Report pdf
  4. ^ Grathwohl, P., 1998. Diffusion in Natural Porous Media: Contaminant Transport, Sorption/Desorption and Dissolution Kinetics. Kluwer Academic Publishers, Boston. DOI: 10.1007/978-1-4615-5683-1 Available from: Springer.com
  5. ^ Carey, G.R., McBean, E.A. and Feenstra, S., 2016. Estimating Tortuosity Coefficients Based on Hydraulic Conductivity. Groundwater, 54(4), pp.476-487. DOI:10.1111/gwat.12406 Available from: NGWA
  6. ^ Fetter, C.W., 1994. Applied Hydrogeology: Macmillan College Publishing Company. New York New York. ISBN-13:978-0130882394
  7. ^ Gelhar, L.W., Gutjahr, A.L. and Naff, R.L., 1979. Stochastic analysis of macrodispersion in a stratified aquifer. Water Resources Research, 15(6), pp.1387-1397. DOI:10.1029/WR015i006p01387
  8. ^ Gelhar, L.W. and Axness, C.L., 1983. Three‐dimensional stochastic analysis of macrodispersion in aquifers. Water Resources Research, 19(1), pp.161-180. DOI:10.1029/WR019i001p00161
  9. ^ 9.0 9.1 Dagan, G., 1988. Time‐dependent macrodispersion for solute transport in anisotropic heterogeneous aquifers. Water Resources Research, 24(9), pp.1491-1500. DOI:10.1029/WR024i009p01491
  10. ^ Zech, A., Attinger, S., Cvetkovic, V., Dagan, G., Dietrich, P., Fiori, A., Rubin, Y. and Teutsch, G., 2015. Is unique scaling of aquifer macrodispersivity supported by field data? Water Resources Research, 51(9), pp.7662-7679. DOI: 10.1002/2015WR017220   Free access article from American Geophysical Union
  11. ^ Payne, F.C., Quinnan, J.A. and Potter, S.T., 2008. Remediation hydraulics. CRC Press. ISBN:978-1-4200-0684-1
  12. ^ Hadley, P.W. and Newell, C., 2014. The new potential for understanding groundwater contaminant transport. Groundwater, 52(2), pp.174-186. doi:10.1111/gwat.12135
  13. ^ Sale, T.C., Illangasekare, T., Zimbron, J., Rodriguez, D., Wilkins, B. and Marinelli, F., 2007. AFCEE source zone initiative. Report Prepared for the Air Force Center for Environmental Excellence by Colorado State University and Colorado School of Mines. Report pdf

See Also

Retrieved from "https://www.enviro.wiki/index.php?title=Dispersion_and_Diffusion&oldid=14202"