User:Jhurley/sandbox

From Enviro Wiki
Revision as of 16:18, 1 February 2024 by Jhurley (talk | contribs) (→‎Electrical Conductivity (EC) Based Technologies)
Jump to: navigation, search

Hydrogeophysical methods for characterization and monitoring of surface water-groundwater interactions

Hydrogeophysical methods can be used to cost-effectively locate and characterize regions of enhanced groundwater/surface-water exchange (GWSWE) and to guide effective follow up investigations based on more traditional invasive methods. The most established methods exploit the contrasts in temperature and/or specific conductance that commonly exist between groundwater and surface water.

Related Article(s):

Contributor(s):

  • Dr. Lee Slater
  • Dr. Ramona Iery
  • Dr. Dimitrios Ntarlagiannis
  • Henry Moore

Key Resource(s):

Introduction

Discharges of contaminated groundwater to surface water bodies threaten ecosystems and degrade the quality of surface water resources. Subsurface heterogeneity associated with the geological setting and stratigraphy often results in such discharges occurring as localized zones (or seeps) of contaminated groundwater. Traditional methods for investigating GWSWE include seepage meters[1][2], which directly quantify the volume flux crossing the bed of a surface water body (i.e, a lake, river or wetland) and point probes that locally measure key water quality parameters (e.g., temperature, pore water velocity, specific conductance, dissolved oxygen, pH). Seepage meters provide direct estimates of seepage fluxes between groundwater and surface- water but are time consuming and can be difficult to deploy in high energy surface water environments and along armored bed sediments. Manual seepage meters rely on quantifying volume changes in a bag of water that is hydraulically connected to the bed. Although automated seepage meters such as the Ultraseep system have been developed, they are generally not suitable for long term deployment (weeks to months). The US Navy has developed the Trident probe for more rapid (relative to seepage meters) sampling, whereby the probe is inserted into the bed and point-in-time pore water quality and sediment parameters are directly recorded (note that the Trident probe does not measure a seepage flux). Such direct probe-based measurements are still relatively time consuming to acquire, particularly when reconnaissance information is required over large areas to determine the location of discrete seeps for further, more quantitative analysis.

Over the last few decades, a broader toolbox of hydrogeophysical technologies has been developed to rapidly and non-invasively evaluate zones of GWSWE in a variety of surface water settings, spanning from freshwater bodies to saline coastal environments. Many of these technologies are currently being deployed under a Department of Defense Environmental Security Technology Certification Program (ESTCP) project (ER21-5237) to demonstrate the value of the toolbox to remedial program managers (RPMs) dealing with the challenge of characterizing surface water contamination via groundwater from facilities proximal to surface water bodies. This article summarizes these technologies and provides references to key resources, mostly provided by the Water Resources Mission Area of the United States Geological Survey that describe the technologies in further detail.

Hydrogeophysical Technologies for Understanding Groundwater-Surface Water Interactions

Hydrogeophysical technologies exploit contrasts in the physical properties between groundwater and surface water to detect and monitor zones of pronounced GWSWE. The two most valuable properties to measure are temperature and electrical conductivity. Temperature has been used for decades as an indicator of groundwater-surface water exchange[3] with early uses including pushing a thermistor into the bed of a surface water body to assess zones of surface water downwelling and groundwater upwelling. Today, a variety of novel technologies that measure temperature over a wide range of spatial and temporal scales are being used to investigate GWSWE. The evaluation of electrical conductivity measurements using point probes and geophysical imaging is also well-established. However, new technologies are now available to exploit electrical conductivity contrasts from GWSWE occurring over a range of spatial and temporal scales.

Temperature-Based Technologies

Several temperature-based GWSWE methodologies exploit the gradient in temperature between surface water and groundwater that exist during certain times of day or seasons of the year. The thermal insulation provided by the Earth’s land surface means that groundwater is warmer than surface water in winter months, but colder than surface water in summer months away from the equator. Therefore, in temperate climates, localized (or ‘preferential’) groundwater discharge into surface water bodies is often observed as cold temperature anomalies in the summer and warm temperature anomalies in the winter. However, there are times of the year such as fall and spring when contrasts in the temperature between groundwater and surface water will be minimal, or even undetectable. These seasonal-driven points in time correspond to the switch in the polarity of the temperature contrast between groundwater and surface water. Consequently, SW to GW gradient temperature-based methods are most effective when deployed at times of the year when the temperature contrasts between groundwater and surface water are greatest. Other time-series temperature monitoring methods depend more on natural daily signals measured at the bed interface and in bed sediments, and those signals may exist year round except where strongly muted by ice cover or surface water stratification. A variety of sensing technologies now exist within the GWSWE toolbox, from techniques that rapidly characterize temperature contrasts over large areas, down to powerful monitoring methods that can continuously quantify GWSWE fluxes at discrete locations identified as hotspots.

Characterization Methods

The primary use of the characterization methods is to rapidly determine precise locations of groundwater upwelling over large areas in order to pinpoint locations for subsequent ground-based observations. A common limitation of these methods is that they can only sense groundwater fluxes into surface water. Methods applied at the water surface and in the surface water column generally cannot detect localized regions of surface water transfer to groundwater, for which temperature measurements collected within the bed sediments are needed. This is a more challenging characterization task that may, in the right conditions, be addressed using electrical conductivity-based methods described later in this article.

Unmanned Aerial Vehicle Infrared (UAV-IR)
Figure 1. UAV IR orthomosaics with estimated scale of (a) a wetland in winter (modified from Briggs et al.[4]) and (b) a mountain stream in summer (modified from Briggs et al.[5]) that both capture multiscale groundwater discharge processes. Figure reproduced from Mangel et al.[6]

Unmanned aerial vehicles (UAVs) equipped with thermal infrared (IR) cameras can provide a very powerful tool for rapidly determining zones of pronounced upwelling of groundwater to surface water. Large areas of can be covered with high spatial resolution. The information obtained can be used to rapidly define locations of focused groundwater upwelling and prioritize these for more intensive surface-based observations (Figure 1). As with all thermal methods, flights must be performed when adequate contrasts in temperature between surface water and groundwater are expected to exist. Not just time of year but, because of the effect of the diurnal temperature signal on surface water bodies, time of day might need to be considered in order to maximize the chance of success. Calibration of UAV-IR camera measurements against simultaneously acquired direct measurements of temperature is recommended to optimize the value of these datasets. UAV-IR methods will not work in all situations. One major limitation of the technology is that the temperature expression of groundwater upwelling must be manifested at the surface of the surface water body. Consequently, the technology will not detect relatively small discharges occurring beneath a relatively deep surface water layer, and thermal imaging over the water surface can be complicated by thermal IR reflection. The chances of success with UAV-IR will be strongest in regions of exposed banks or shallow water where there are no strong currents causing mixing (and thus dilution) of the upwelling groundwater temperature signals. UAV-IR methods will therefore likely be most successful close to shorelines of lakes/ponds, over shallow, low flow streams and rivers and in wetland environments. UAV-IR methods require a licensed pilot, and restrictions on the use of airspace may limit the application of this technology.

Handheld Thermal Infrared (TIR) Cameras
Figure 2. (a) A TIR camera set up to image groundwater discharges to surface water (b) TIR data inset on a visible light photograph. Cooler (blue) bank seepage groundwater is discharging into warmer (red) stream water (temperature scale in degrees). Both photographs courtesy of Martin Briggs USGS.

Hand-held thermal infrared (TIR) cameras are powerful tools for visual identification of localized seeps of upwelling groundwater. TIR cameras may be used to follow up on UAV-IR surveys to better characterize local seeps identified from the air using UAV-IR. Alternatively, a TIR camera is a valuable tool when performing initial walks of prospective study sites as they may quickly confirm the presence of suspected seeps. TIR cameras provide high resolution images that can define the structure of localized seeps and may provide valuable insights into the role of discrete features (e.g., fractures in rocks or pipes in soil) in determining seep morphology (Figure 2). Like UAV-IR, TIR provides primarily qualitative information (location, extent) of seeps and it only succeeds when there are adequate contrasts between groundwater and surface water that are expressed at the surface of the investigated water body or along bank sediments. The United States Geological Survey (USGS) has made extensive use of TIR cameras for studying groundwater/surface-water exchange.

Continuous Near-bed Temperature Sensing

When performing surveys from a boat a simple yet often powerful technology is continuous near-bed temperature sensing, whereby a temperature probe is strategically suspended to float in the water column just above the bed or dragged along it. Compared to UAV-IR, this approach does not rely on upwelling groundwater being expressed as a temperature anomaly at the surface. The utility of the method can be enhanced when a specific conductance probe is co- located with the temperature probe so that anomalies in both temperature and specific conductance can be investigated.

Monitoring Methods

Monitoring methods allow temperature signals to be recorded with high temporal resolution along the bed interface or within bank or bed sediments. These methods can capture temporal trends in GWSWE driven by variations in the hydraulic gradients around surface water bodies, as well as changes in hydraulic conductivity due to sedimentation, clogging, scour or microbial mass. If vertical profiles of bed temperature are collected, a range of analytical and numerical models can be applied to infer the vertical water flux rate and direction, similar to a seepage meter. These fluxes may vary as a function of season, rainfall events (enhanced during storm activity), tidal variability in coastal settings and due to engineered controls such as dam discharges. The methods can capture evidence of GWSWE that may not be detected during a single ‘characterization’ survey if the local hydraulic conditions at that point in time result in relatively weak hydraulic gradients.

Fiber-optic Distributed Temperature Sensing (FO-DTS)
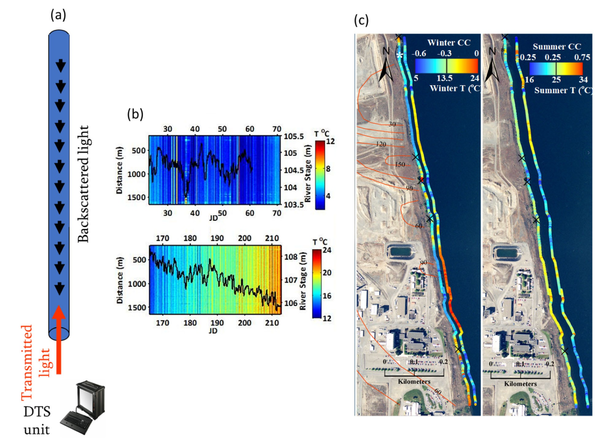
Figure 3. (a) Basic concept of FO-DTS based on backscattering of light transmitted down a FO fiber (b) Example of riverbed temperature data acquired over time and space in relation to variation in river stage (black line) modified from Mwakanyamale et al.[7] (c) spatial distribution of riverbed temperature and correlation coefficient (CC) between riverbed temperature and river stage for a 1.5 km stretch along the Hanford 300 Area adjacent to the Columbia River (modified from Slater et al.[8]). Data are shown for winter and summer. Orange contours show uranium concentrations (μg/L) in groundwater measured in boreholes.

Fiber-optic distributed temperature sensing (FO-DTS) is a powerful monitoring technology used in fire detection, industrial process monitoring, and petroleum reservoir monitoring. The method is also used to obtain spatially rich datasets for monitoring GWSWE[9][10]. The sensor consists of standard telecommunications fiber-optic fiber typically housed in armored cable and the physics is based on temperature-dependent backscatter mechanisms including Brillouin and Raman backscatter[9]. Most commercially available systems are based on analysis of Raman scatter. As laser light is transmitted down the fiber-optic cable, light scatters continuously back toward the instrument from all along the fiber, with some of the scattered light at frequencies above and below the frequency of incident light, i.e., anti-Stokes and Stokes-Raman backscatter, respectively. The ratio of anti-Stokes to Stokes energy provides the basis for FO-DTS measurements. Measurements are localized to a section of cable according to a time-of-flight calculation (i.e., optical time-domain reflectometry). Assuming the speed of light within the fiber is constant, scatter collected over a specific time window corresponds to a specific spatial interval of the fiber. Although there are tradeoffs between spatial resolution, thermal precision, and sampling time, in practice it is possible to achieve sub meter-scale spatial and approximate 0.1°C thermal precision for measurement cycle times on the order of minutes and cables extending several kilometers[10]; thus, thousands of temperature measurements can be made simultaneously along a single cable. The method allows the visualization of a large amount of temperature data and rapid identification of major trends in GWSWE. Figure 3 illustrates the use of FO-DTS to detect and monitor zones of focused groundwater discharge along a 1.5 km reach of the Columbia River that is threatened by contaminated groundwater[8]. As temperature is only sensed at the cable on the bed, FO-DTS can only detect groundwater inputs to surface water. It cannot detect losses of surface water to groundwater. The USGS public domain software tool DTSGUI allows a user to import, manage, visualize and analyze FO-DTS datasets.

Vertical temperature profilers (VTPs)

Analysis methods now allow for the accurate quantification of groundwater fluxes over time. Vertical temperature profilers (VTPs) are sensors applied for diurnal temperature data collection within saturated geologic matrices (Figure 4). Extensive experience with VTPs indicates that the methodology is equal to traditional seepage meters in terms of flux accuracy[11]. However, VTPs have the advantage of measuring continuous temporal variations in flux rates while such information is impractical to obtain with traditional seepage meters.

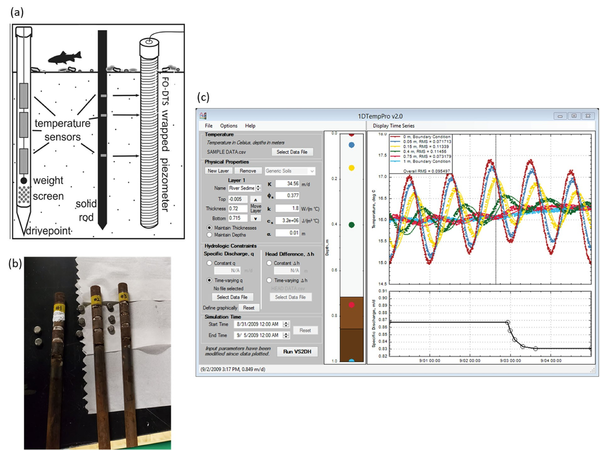
Figure 4. (a) Schematic of different VTP setups including (from left to right) thermistors in a piezometer, thermistors embedded in a solid rod and wrapped FO-DTS cable modified from Irvine et al.[12]; (b) construction of VTPs showing thermistors embedded in rods and subsequent insulation; (c) example dataset plotted in 1DTempPro showing 5 days of streambed temperature at 6 streambed depths[13].

The low-cost design, ease of data collection, and straightforward interpretation of the data using open-source software make VTP sensors increasingly attractive for quantifying flux rates. These sensors typically consist of at least two temperature loggers installed within a steel or plastic pipe filled with foam insulation[12] although the use of loggers installed in well screens or FO-DTS cable wrapped around a piezometer casing (for high vertical resolution data) are also possible (Figure 4a). Loggers are inserted into the insulated housing at different depths, typically starting from one centimeter within the geologic matrix of interest[14]. Temperature loggers usually remain within the first 0.2-meters of the geologic matrix based on the observed limits of diurnal signal influence[15], though zones of strong surface water downwelling may necessitate deeper temperature data collection. Reliability of flux values generated from the temperature signal analysis is dependent in part on the temperature logger precision, VTP placement, sediment heterogeneity, flow direction, flow magnitude[14], and absence of macropore flow. Application of single dimension temperature-based fluid flux models assumes that all flow is vertical and therefore lateral flow within upwelling systems cannot be quantified using VTPs, emphasizing the importance of the VTP installation location over the active area of exchange[14] at shallow depths. Thermal parameters of the geologic matrix where the VTP is installed can be measured using a thermal properties analyzer to record heat capacity and thermal conductivity for later analytical and numerical modeling.

Analytical and numerical solutions, used to solve or estimate the advection-conduction equation within the geologic matrix (bed sediments), continue to evolve to better quantify flux values over time. Analytical solutions to the heat transport equation are used to solve for flux values between sensor pairs from VTP datasets[16][17]. VFLUX is an open-source MATLAB package that allows the user to solve for flux values from a VTP dataset using a variety of analytical solutions[16][17] based on the vertical propagation of diurnal temperature signals. Other emerging ‘spectral’ methods make use of a wide range of natural temperature signals to estimate vertical flux and bed sediment thermal diffusivity[18]. VFLUX analytical solutions are limited by subsurface heterogeneity and diurnal temperature signal strength[14]. 1DTempPro (Figure 4c) provides a graphical user interface (GUI) for numerical solutions to heat transport[19] and does not depend on diurnal signals. Numerical models can produce more accurate flux estimates in the case of complex boundary conditions and abrupt changes in flux rates, but require significant user calibration efforts for longer time series[20]. A hybrid approach between the analytical and numerical solutions, known as tempest1d[20] improves flux modeling with enhanced computational efficiency, resolution of abrupt changes, evaluation of complex boundary conditions, and uncertainty estimations with each step. This new state-space modeling approach uses recursive estimation techniques to automatically estimate highly dynamic vertical flux patterns ranging from sub-daily to seasonal time scales[20].

Electrical Conductivity (EC) Based Technologies

The electrical conductivity (EC)-based technologies exploit contrasts in EC between surface water and groundwater[21]. EC-based technologies are mostly applied as characterization tools, although the opportunity to monitor GWSWE dynamics with one of these technologies does exist. With the exception of specific conductance probes, the technologies measure the bulk EC of sediments, which will often (but not always) reveal evidence of GWSWE.

Electrical conduction (i.e., the transport of charges) in the Earth occurs via the ions dissolved in groundwater, with an additional contribution from ions in the electrical double layer (known as surface conduction)[22]. In relatively fresh surface water environments, groundwater is typically more electrically conductive than surface water due to the higher ion concentrations in groundwater. In these settings, groundwater inputs may be identified as zones of higher bulk EC beneath the bed. In coastal settings where surface water is saline, inputs of relatively fresh groundwater will give rise to zones of lower conductivity. Whereas the temperature-based methods rely on point measurements at the location of the sensor, the EC-based technologies (with the exception of point specific conductance measurements) incorporate inverse modeling to estimate distributions of EC away from the sensors and beneath the bed. Consequently, these technologies may also image losses of surface water to groundwater[23]. Another advantage is that they may provide information on structural controls on zones of focused GWSWE expressed at the surface. However, interpretation of EC patterns from these technologies is inherently uncertain due to the fact that (with the exception of specific conductance probes) the bulk EC of the sediments is measured. Variations in lithology (e.g., porosity, grain size distribution, which determine the strength of surface conduction) can be misinterpreted as variations in the ionic composition of groundwater.

Characterization Methods

Specific Conductance Probes

The simplest EC-based technology is a specific conductance probe, which measures the specific conductance of water between a small pair of metal plates at the end of the sensor probe. Many commercially available water quality sensors have a specific conductance sensor and a temperature sensor integrated into a single probe (they often also measure other water quality parameters, including pH and dissolved oxygen (DO) content). These are direct sensing measurements with a small footprint (the size of the sensor), so this is usually a time-consuming, inefficient method for detecting GWSWE dynamics. Furthermore, the sampling volume of the measurement is small (on the order of a cubic centimeter or less), so the degree to which the spot measurement is representative of larger-scale hydrological exchanges is often uncertain. However, specific conductance sensor remains popular, especially when integrated with a point temperature sensor, such as the Trident Probe.

Frequency Domain Electromagnetic (EM) Sensing Systems
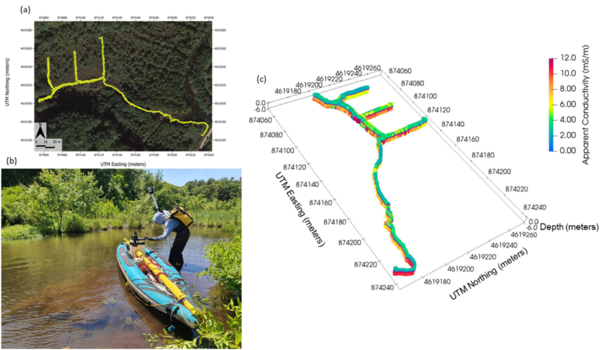
Figure 5. (a) FDEM survey path within a stream/drainage channel network bisecting a wetland complex experiencing localized upwelling of contaminated groundwater (b) operation of an FDEM sensor (Dualem 421S, Dualem, CA) in this shallow stream environment (c) resulting imaging of EC structure in the upper 6 m of streambed sediments. Variations in EC may result from changes in sediment texture that determine the location of focused GWSWE. Dataset acquired under ESTCP project ER21-5237.

Electromagnetic (EM) sensors non-invasively sense the bulk EC of sediments (a function of both fluid composition and lithology as mentioned above) by measuring eddy currents induced in conductors using time varying electric and magnetic fields based on the physics of electromagnetic induction. Modern EM systems can simultaneously image across a range of depths. Frequency domain EM (FDEM) instruments generate a current that varies sinusoidally with time at a fixed frequency that is selected on the basis of desired exploration depth and resolution. State of the art FDEM sensors use a combination of different coil separations and/or frequencies to resolve conductivity structure over a range of depths. These instruments typically provide high-resolution (sub-meter) information on the EC structure in the upper 5 m (approximately, depending on EC) of the subsurface. Measurements are non-invasively and continuously made, meaning that large areas can be quickly surveyed on foot (e.g., along a shoreline) or from a boat in shallow water (1 m or less deep), for example when pulled along a river or stream channel. The method can also be deployed effectively in wetlands (Figure 5). FDEM data are often presented in terms of variations in the raw measurements because apparent EC values do not represent the true EC of the subsurface. However, with the increasing popularity of sensors with combinations of coil separations, the datasets can be inverted to obtain a model of the distribution of the true EC of the subsurface on land or below a water layer. Inversion of FDEM datasets is usually performed as a series of one-dimensional (1D) models, constrained to have a limited variance from each other, to generate a pseudo-2D model of the subsurface. Open-source software, such as EMagPy[24], is freely available to manage, visualize and interpret FDEM datasets.

Time Domain EM Sensing Systems

Time domain EM (TEM) systems transmit a current that is abruptly shut off (reduced to zero), resulting in a transient current flow that propagates (with decaying amplitude) into the earth. The time-decaying voltage recorded in a receiver coil contains information on the EC variation with depth below the instrument. TEM systems specifically designed for waterborne surveys provide investigation depths up to 70 m (again depending on electrical conductivity)[25]. Airborne TEM systems can also be deployed to look at large-scale surface water/groundwater dynamics, for example submarine discharge or saline intrusion along coastlines[26]. Inverse methods are employed to convert the raw measurements obtained along a transect into a distribution of conductivity.

Waterborne Electrical Imaging
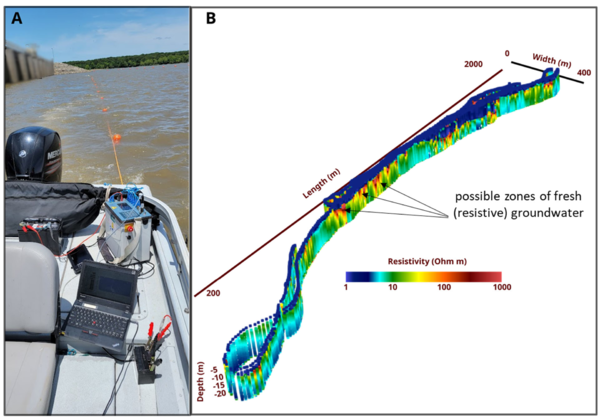
Figure 6. Waterborne electrical imaging in a coastal setting with expected zones of upwelling groundwater (a) typical operation with floating electrode cable pulled behind boat (b) inverted 2D cross section of electrical resistivity along the survey path with possible zones of fresh groundwater discharges indicated from relatively high resistivity sediments. Dataset acquired under ESTCP project ER21-5237.

Electrical imaging techniques are based on galvanic (direct) contact between electrodes used to inject currents (and measure voltages) and the subsurface[22]. Relative to EM methods, this can be a disadvantage when surveying on land. However, when making measurements from a water body, the electrodes used to acquire the data can be deployed as a floating array that is pulled behind a vessel. Waterborne electrical imaging relies on acquiring measurements of electrical potential differences between different pairs of electrodes on the array while current is passed between one pair of electrodes[27]. As the array is pulled behind the boat, thousands of measurements are made along a survey transect. Similar to the EM methods, inverse methods are used to process these datasets and generate a 2D image of the variation in the conductivity of the sediments below the bed. Open-source software such as ResIPy support 2D or 3D inversion of waterborne datasets. Figure 6 shows results of a waterborne electrical imaging survey conducted to locate regions where relative fresh (electrically resistive) groundwater is discharging into the near shore environment in a coastal setting. Beneath the saline (low resistivity) water layer, spatial variability in resistivity may partly be related to variations in the pore-filling fluid conductivity, with localized resistive zones possibly indicating upwelling fresh groundwater. However, the variation in resistivity in the sediments below the water layer may reflect variations in lithology. An extension of the electrical imaging method involves collecting induced polarization (IP) data[22] in addition to electrical resistivity data. IP measurements capture the temporary charge storage characteristics of the subsurface, which are strongly controlled by lithology, with finer-grained (e.g. clay rich) sediments being more chargeable than coarser grained sediments. The method can be particularly useful for differentiating between conductivity variations resulting from variations in pore fluid specific conductance and those conductivity variations associated with lithology. For example, based on electrical imaging methods alone (or the EM method alone), it may not be possible to distinguish a zone of high specific conductance groundwater entering into freshwater from a region of relatively finer- grained sediments without additional supporting data (e.g. a core). IP measurements may be able to resolve this ambiguity as the region of finer-grained sediments will be more chargeable than the surrounding areas.

Monitoring Methods

Land-based Electrical Monitoring

There is increasing interest in the use of electrical imaging methods as monitoring systems. Semi-permanent arrays of electrodes can be installed to monitor groundwater/surface water dynamics over periods of days to years. Low-power instrumentation has been developed to specifically address the needs for long-term monitoring, although such instrumentation is not yet commercially available. Consequently, electrical monitoring of groundwater/surface water interactions currently remains in the realm of the research-driven specialist.

Considerations for Using EM and Waterborne Electrical Imaging Methods

The EM and waterborne electrical imaging methods both provide a way to determine variations in bulk electrical conductivity associated with groundwater/surface water interactions. However, each method has some advantages and some disadvantages. One consideration is maneuverability, particularly in shallow water environments. FDEM instruments are the most maneuverable, although they offer only limited investigation depths. Although bigger than the shallow-sensing frequency domain EM systems, TEM systems are still relatively maneuverable on water bodies. Whereas FDEM systems can be operated from a single small vessel, the TEM deployments require the use of pontoons as the transmitter and receiver coils need to be separated 9 m apart. This still equates to good maneuverability compared to waterborne electrical imaging where a floating electrode cable, typically 30-50 m long, is pulled behind a vessel.

In all three methods, variations in the water layer depth and the specific conductance of the water can significantly affect the data, especially in deeper water. Therefore, it is common to continuously record these parameters with an echo sounder and a specific conductance probe suspended in the water layer.

Other Hydrogeophysical Technologies

A number of other hydrogeophysical technologies exist, with proven applications to the characterization of settings where GWSWE occurs. Seismic


Hydroquinones have been widely used as surrogates to understand the reductive transformation of NACs and MCs by NOM. Figure 4 shows the chemical structures of the singly deprotonated forms of four hydroquinone species previously used to study NAC/MC reduction. The second-order rate constants (kR) for the reduction of NACs/MCs by these hydroquinone species are listed in Table 1, along with the aqueous-phase one electron reduction potentials of the NACs/MCs (EH1’) where available. EH1’ is an experimentally measurable thermodynamic property that reflects the propensity of a given NAC/MC to accept an electron in water (EH1(R-NO2)):

Equation 1:                R-NO2 + e- ⇔ R-NO2•-

Knowing the identity of and reaction order in the reductant is required to derive the second-order rate constants listed in Table 1. This same reason limits the utility of reduction rate constants measured with complex carbonaceous reductants such as NOM[28], BC[29][30][31][32], and HS[33][34], whose chemical structures and redox moieties responsible for the reduction, as well as their abundance, are not clearly defined or known. In other words, the observed rate constants in those studies are specific to the experimental conditions (e.g., pH and NOM source and concentration), and may not be easily comparable to other studies.

Table 1. Aqueous phase one electron reduction potentials and logarithm of second-order rate constants for the reduction of NACs and MCs by the singly deprotonated form of the hydroquinones lawsone, juglone, AHQDS and AHQS, with the second-order rate constants for the deprotonated NAC/MC species (i.e., nitrophenolates and NTO–) in parentheses.
Compound EH1' (V) Hydroquinone [log kR (M-1s-1)]
(NAC/MC) LAW- JUG- AHQDS- AHQS-
Nitrobenzene (NB) -0.485[35] 0.380[35] -1.102[35] 2.050[36] 3.060[36]
2-nitrotoluene (2-NT) -0.590[35] -1.432[35] -2.523[35] 0.775[37]
3-nitrotoluene (3-NT) -0.475[35] 0.462[35] -0.921[35]
4-nitrotoluene (4-NT) -0.500[35] 0.041[35] -1.292[35] 1.822[37] 2.610[36]
2-chloronitrobenzene (2-ClNB) -0.485[35] 0.342[35] -0.824[35] 2.412[37]
3-chloronitrobenzene (3-ClNB) -0.405[35] 1.491[35] 0.114[35]
4-chloronitrobenzene (4-ClNB) -0.450[35] 1.041[35] -0.301[35] 2.988[37]
2-acetylnitrobenzene (2-AcNB) -0.470[35] 0.519[35] -0.456[35]
3-acetylnitrobenzene (3-AcNB) -0.405[35] 1.663[35] 0.398[35]
4-acetylnitrobenzene (4-AcNB) -0.360[35] 2.519[35] 1.477[35]
2-nitrophenol (2-NP) 0.568 (0.079)[35]
4-nitrophenol (4-NP) -0.699 (-1.301)[35]
4-methyl-2-nitrophenol (4-Me-2-NP) 0.748 (0.176)[35]
4-chloro-2-nitrophenol (4-Cl-2-NP) 1.602 (1.114)[35]
5-fluoro-2-nitrophenol (5-Cl-2-NP) 0.447 (-0.155)[35]
2,4,6-trinitrotoluene (TNT) -0.280[38] 2.869[39] 5.204[37]
2-amino-4,6-dinitrotoluene (2-A-4,6-DNT) -0.400[38] 0.987[39]
4-amino-2,6-dinitrotoluene (4-A-2,6-DNT) -0.440[38] 0.079[39]
2,4-diamino-6-nitrotoluene (2,4-DA-6-NT) -0.505[38] -1.678[39]
2,6-diamino-4-nitrotoluene (2,6-DA-4-NT) -0.495[38] -1.252[39]
1,3-dinitrobenzene (1,3-DNB) -0.345[39] 1.785[39]
1,4-dinitrobenzene (1,4-DNB) -0.257[39] 3.839[39]
2-nitroaniline (2-NANE) < -0.560[39] -2.638[39]
3-nitroaniline (3-NANE) -0.500[39] -1.367[39]
1,2-dinitrobenzene (1,2-DNB) -0.290[39] 5.407[37]
4-nitroanisole (4-NAN) -0.661[36] 1.220[36]
2-amino-4-nitroanisole (2-A-4-NAN) -0.924[36] 1.150[36] 2.190[36]
4-amino-2-nitroanisole (4-A-2-NAN) 1.610[36] 2.360[36]
2-chloro-4-nitroaniline (2-Cl-5-NANE) -0.863[36] 1.250[36] 2.210[36]
N-methyl-4-nitroaniline (MNA) -1.740[36] -0.260[36] 0.692[36]
3-nitro-1,2,4-triazol-5-one (NTO) 5.701 (1.914)[34]
Hexahydro-1,3,5-trinitro-1,3,5-triazine (RDX) -0.349[40]
Figure 5. Relative reduction rate constants of the NACs/MCs listed in Table 1 for AHQDS–. Rate constants are compared with respect to RDX. Abbreviations of NACs/MCs as listed in Table 1.

Most of the current knowledge about MC degradation is derived from studies using NACs. The reduction kinetics of only four MCs, namely TNT, N-methyl-4-nitroaniline (MNA), NTO, and RDX, have been investigated with hydroquinones. Of these four MCs, only the reduction rates of MNA and TNT have been modeled[39][36][41][42].

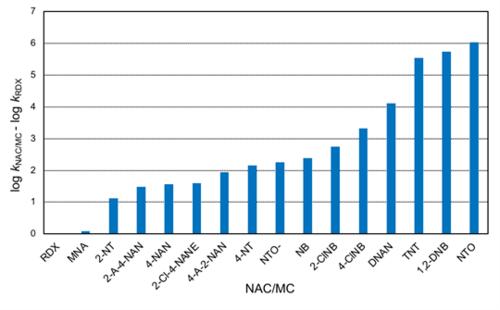
Using the rate constants obtained with AHQDS–, a relative reactivity trend can be obtained (Figure 5). RDX is the slowest reacting MC in Table 1, hence it was selected to calculate the relative rates of reaction (i.e., log kNAC/MC – log kRDX). If only the MCs in Figure 5 are considered, the reactivity spans 6 orders of magnitude following the trend: RDX ≈ MNA < NTO– < DNAN < TNT < NTO. The rate constant for DNAN reduction by AHQDS– is not yet published and hence not included in Table 1. Note that speciation of NACs/MCs can significantly affect their reduction rates. Upon deprotonation, the NAC/MC becomes negatively charged and less reactive as an oxidant (i.e., less prone to accept an electron). As a result, the second-order rate constant can decrease by 0.5-0.6 log unit in the case of nitrophenols and approximately 4 log units in the case of NTO (numbers in parentheses in Table 1)[35][34].

Ferruginous Reductants

Table 2. Logarithm of second-order rate constants for reduction of NACs and MCs by dissolved Fe(II) complexes with the stoichiometry of ligand and iron in square brackets
Compound EH1' (V) Cysteine[43]
[FeL2]2- 		Thioglycolic acid[43]
[FeL2]2- 		DFOB[44]
[FeHL]0 		AcHA[44]
[FeL3]- 		Tiron a
[FeL2]6- 		Fe-Porphyrin b
Fe(II)-Ligand [log kR (M-1s-1)]
Nitrobenzene -0.485[35] -0.347 0.874 2.235 -0.136 1.424[45]
4.000[42]		 -0.018[35]
0.026[42]
2-nitrotoluene -0.590[35] -0.602[35]
3-nitrotoluene -0.475[35] -0.434 0.767 2.106 -0.229 1.999[45]
3.800[42]		 0.041[35]
4-nitrotoluene -0.500[35] -0.652 0.528 2.013 -0.402 1.446[45]
3.500[42]		 -0.174[35]
2-chloronitrobenzene -0.485[35] 0.944[35]
3-chloronitrobenzene -0.405[35] 0.360 1.810 2.888 0.691 2.882[45]
4.900[42]		 0.724[35]
4-chloronitrobenzene -0.450[35] 0.230 1.415 2.512 0.375 3.937[45]
4.581[46]		 0.431[35]
0.289[42]
2-acetylnitrobenzene -0.470[35] 1.377[35]
3-acetylnitrobenzene -0.405[35] 0.799[35]
4-acetylnitrobenzene -0.360[35] 0.965 2.771 1.872 5.028[45]
6.300[42]		 1.693[35]
RDX -0.550[47] 2.212[45]
2.864[48]
HMX -0.660[47] -2.762[45]
TNT -0.280[38] 7.427[45] 2.050[42]
1,3-dinitrobenzene -0.345[39] 1.220[42]
2,4-dinitrotoluene -0.380[38] 5.319[45] 1.156[42]
Nitroguanidine (NQ) -0.700[47] -0.185[45]
2,4-dinitroanisole (DNAN) -0.400[47] 1.243[42]
Notes:
a 4,5-dihydroxybenzene-1,3-disulfonate (Tiron). b meso-tetra(N-methyl-pyridyl)iron porphin in cysteine.
Table 3. Rate constants for the reduction of MCs by iron minerals
MC Iron Mineral Iron mineral loading
(g/L) 		Surface area
(m2/g) 		Fe(II)aq initial
(mM) b 		Fe(II)aq after 24 h
(mM) c 		Fe(II)aq sorbed
(mM) d 		pH Buffer Buffer
(mM) 		MC initial
(μM) e 		log kobs
(h-1) f 		log kSA
(Lh-1m-2) g
TNT[39] Goethite 0.64 17.5 1.5 7.0 MOPS 25 50 1.200 0.170
RDX[49] Magnetite 1.00 44 0.1 0 0.10 7.0 HEPES 50 50 -3.500 -5.200
RDX[49] Magnetite 1.00 44 0.2 0.02 0.18 7.0 HEPES 50 50 -2.900 -4.500
RDX[49] Magnetite 1.00 44 0.5 0.23 0.27 7.0 HEPES 50 50 -1.900 -3.600
RDX[49] Magnetite 1.00 44 1.5 0.94 0.56 7.0 HEPES 50 50 -1.400 -3.100
RDX[49] Magnetite 1.00 44 3.0 1.74 1.26 7.0 HEPES 50 50 -1.200 -2.900
RDX[49] Magnetite 1.00 44 5.0 3.38 1.62 7.0 HEPES 50 50 -1.100 -2.800
RDX[49] Magnetite 1.00 44 10.0 7.77 2.23 7.0 HEPES 50 50 -1.000 -2.600
RDX[49] Magnetite 1.00 44 1.6 1.42 0.16 6.0 MES 50 50 -2.700 -4.300
RDX[49] Magnetite 1.00 44 1.6 1.34 0.24 6.5 MOPS 50 50 -1.800 -3.400
RDX[49] Magnetite 1.00 44 1.6 1.21 0.37 7.0 MOPS 50 50 -1.200 -2.900
RDX[49] Magnetite 1.00 44 1.6 1.01 0.57 7.0 HEPES 50 50 -1.200 -2.800
RDX[49] Magnetite 1.00 44 1.6 0.76 0.82 7.5 HEPES 50 50 -0.490 -2.100
RDX[49] Magnetite 1.00 44 1.6 0.56 1.01 8.0 HEPES 50 50 -0.590 -2.200
NG[50] Magnetite 4.00 0.56 4.0 7.4 HEPES 90 226
NG[51] Pyrite 20.00 0.53 7.4 HEPES 100 307 -2.213 -3.238
TNT[51] Pyrite 20.00 0.53 7.4 HEPES 100 242 -2.812 -3.837
RDX[51] Pyrite 20.00 0.53 7.4 HEPES 100 201 -3.058 -4.083
RDX[52] Carbonate Green Rust 5.00 36 7.0 100
RDX[52] Sulfate Green Rust 5.00 20 7.0 100
DNAN[53] Sulfate Green Rust 10.00 8.4 500
NTO[53] Sulfate Green Rust 10.00 8.4 500
DNAN[54] Magnetite 2.00 17.8 1.0 7.0 NaHCO3 10 200 -0.100 -1.700
DNAN[54] Mackinawite 1.50 7.0 NaHCO3 10 200 0.061
DNAN[54] Goethite 1.00 103.8 1.0 7.0 NaHCO3 10 200 0.410 -1.600
RDX[55] Magnetite 0.62 1.0 7.0 NaHCO3 10 17.5 -1.100
RDX[55] Magnetite 0.62 7.0 MOPS 50 17.5 -0.270
RDX[55] Magnetite 0.62 1.0 7.0 MOPS 10 17.6 -0.480
NTO[56] Hematite 1.00 5.7 1.0 0.92 0.08 5.5 MES 50 30 -0.550 -1.308
NTO[56] Hematite 1.00 5.7 1.0 0.85 0.15 6.0 MES 50 30 0.619 -0.140
NTO[56] Hematite 1.00 5.7 1.0 0.9 0.10 6.5 MES 50 30 1.348 0.590
NTO[56] Hematite 1.00 5.7 1.0 0.77 0.23 7.0 MOPS 50 30 2.167 1.408
NTO[56] Hematite a 1.00 5.7 1.01 5.5 MES 50 30 -1.444 -2.200
NTO[56] Hematite a 1.00 5.7 0.97 6.0 MES 50 30 -0.658 -1.413
NTO[56] Hematite a 1.00 5.7 0.87 6.5 MES 50 30 0.068 -0.688
NTO[56] Hematite a 1.00 5.7 0.79 7.0 MOPS 50 30 1.210 0.456
RDX[57] Mackinawite 0.45 6.5 NaHCO3 10 250 -0.092
RDX[57] Mackinawite 0.45 7.0 NaHCO3 10 250 0.009
RDX[57] Mackinawite 0.45 7.5 NaHCO3 10 250 0.158
RDX[57] Green Rust 5 6.5 NaHCO3 10 250 -1.301
RDX[57] Green Rust 5 7.0 NaHCO3 10 250 -1.097
RDX[57] Green Rust 5 7.5 NaHCO3 10 250 -0.745
RDX[57] Goethite 0.5 1 1 6.5 NaHCO3 10 250 -0.921
RDX[57] Goethite 0.5 1 1 7.0 NaHCO3 10 250 -0.347
RDX[57] Goethite 0.5 1 1 7.5 NaHCO3 10 250 0.009
RDX[57] Hematite 0.5 1 1 6.5 NaHCO3 10 250 -0.824
RDX[57] Hematite 0.5 1 1 7.0 NaHCO3 10 250 -0.456
RDX[57] Hematite 0.5 1 1 7.5 NaHCO3 10 250 -0.237
RDX[57] Magnetite 2 1 1 6.5 NaHCO3 10 250 -1.523
RDX[57] Magnetite 2 1 1 7.0 NaHCO3 10 250 -0.824
RDX[57] Magnetite 2 1 1 7.5 NaHCO3 10 250 -0.229
DNAN[58] Mackinawite 4.28 0.25 6.5 NaHCO3 8.5 + 20% CO2(g) 400 0.836 0.806
DNAN[58] Mackinawite 4.28 0.25 7.6 NaHCO3 95.2 + 20% CO2(g) 400 0.762 0.732
DNAN[58] Commercial FeS 5.00 0.214 6.5 NaHCO3 8.5 + 20% CO2(g) 400 0.477 0.447
DNAN[58] Commercial FeS 5.00 0.214 7.6 NaHCO3 95.2 + 20% CO2(g) 400 0.745 0.716
NTO[58] Mackinawite 4.28 0.25 6.5 NaHCO3 8.5 + 20% CO2(g) 1000 0.663 0.633
NTO[58] Mackinawite 4.28 0.25 7.6 NaHCO3 95.2 + 20% CO2(g) 1000 0.521 0.491
NTO[58] Commercial FeS 5.00 0.214 6.5 NaHCO3 8.5 + 20% CO2(g) 1000 0.492 0.462
NTO[58] Commercial FeS 5.00 0.214 7.6 NaHCO3 95.2 + 20% CO2(g) 1000 0.427 0.398
Notes:
a Dithionite-reduced hematite; experiments conducted in the presence of 1 mM sulfite. b Initial aqueous Fe(II); not added for Fe(II) bearing minerals. c Aqueous Fe(II) after 24h of equilibration. d Difference between b and c. e Initial nominal MC concentration. f Pseudo-first order rate constant. g Surface area normalized rate constant calculated as kObs / (surface area concentration) or kObs / (surface area × mineral loading).
Table 4. Rate constants for the reduction of NACs by iron oxides in the presence of aqueous Fe(II)
NAC a Iron Oxide Iron oxide loading
(g/L) 		Surface area
(m2/g) 		Fe(II)aq initial
(mM) b 		Fe(II)aq after 24 h
(mM) c 		Fe(II)aq sorbed
(mM) d 		pH Buffer Buffer
(mM) 		NAC initial
(μM) e 		log kobs
(h-1) f 		log kSA
(Lh-1m-2) g
NB[59] Magnetite 0.200 56.00 1.5000 7.00 Phosphate 10 50 1.05E+00 7.75E-04
4-ClNB[59] Magnetite 0.200 56.00 1.5000 7.00 Phosphate 10 50 1.14E+00 8.69E-02
4-ClNB[39] Goethite 0.640 17.50 1.5000 7.00 MOPS 25 50 -1.01E-01 -1.15E+00
4-ClNB[60] Goethite 1.500 16.20 1.2400 0.9600 0.2800 7.20 MOPS 1.2 0.5 - 3 1.68E+00 2.80E-01
4-ClNB[60] Hematite 1.800 13.70 1.0400 1.0100 0.0300 7.20 MOPS 1.2 0.5 - 3 -2.32E+00 -3.72E+00
4-ClNB[60] Lepidocrocite 1.400 17.60 1.1400 1.0000 0.1400 7.20 MOPS 1.2 0.5 - 3 1.51E+00 1.20E-01
4-CNNB[61] Ferrihydrite 0.004 292.00 0.3750 0.3500 0.0300 7.97 HEPES 25 15 -7.47E-01 -8.61E-01
4-CNNB[61] Ferrihydrite 0.004 292.00 0.3750 0.3700 0.0079 7.67 HEPES 25 15 -1.51E+00 -1.62E+00
4-CNNB[61] Ferrihydrite 0.004 292.00 0.3750 0.3600 0.0200 7.50 MOPS 25 15 -2.15E+00 -2.26E+00
4-CNNB[61] Ferrihydrite 0.004 292.00 0.3750 0.3600 0.0120 7.28 MOPS 25 15 -3.08E+00 -3.19E+00
4-CNNB[61] Ferrihydrite 0.004 292.00 0.3750 0.3700 0.0004 7.00 MOPS 25 15 -3.22E+00 -3.34E+00
4-CNNB[61] Ferrihydrite 0.004 292.00 0.3750 0.3700 0.0024 6.80 MOPSO 25 15 -3.72E+00 -3.83E+00
4-CNNB[61] Ferrihydrite 0.004 292.00 0.3750 0.3700 0.0031 6.60 MES 25 15 -3.83E+00 -3.94E+00
4-CNNB[61] Ferrihydrite 0.020 292.00 0.3750 0.3700 0.0031 6.60 MES 25 15 -3.83E+00 -4.60E+00
4-CNNB[61] Ferrihydrite 0.110 292.00 0.3750 0.3700 0.0032 6.60 MES 25 15 -1.57E+00 -3.08E+00
4-CNNB[61] Ferrihydrite 0.220 292.00 0.3750 0.3700 0.0040 6.60 MES 25 15 -1.12E+00 -2.93E+00
4-CNNB[61] Ferrihydrite 0.551 292.00 0.3750 0.3700 0.0092 6.60 MES 25 15 -6.18E-01 -2.82E+00
4-CNNB[61] Ferrihydrite 1.099 292.00 0.3750 0.3500 0.0240 6.60 MES 25 15 -3.66E-01 -2.87E+00
4-CNNB[61] Ferrihydrite 1.651 292.00 0.3750 0.3400 0.0340 6.60 MES 25 15 -8.35E-02 -2.77E+00
4-CNNB[61] Ferrihydrite 2.199 292.00 0.3750 0.3300 0.0430 6.60 MES 25 15 -3.11E-02 -2.84E+00
4-CNNB[61] Hematite 0.038 34.00 0.3750 0.3320 0.0430 7.97 HEPES 25 15 1.63E+00 1.52E+00
4-CNNB[61] Hematite 0.038 34.00 0.3750 0.3480 0.0270 7.67 HEPES 25 15 1.26E+00 1.15E+00
4-CNNB[61] Hematite 0.038 34.00 0.3750 0.3470 0.0280 7.50 MOPS 25 15 7.23E-01 6.10E-01
4-CNNB[61] Hematite 0.038 34.00 0.3750 0.3680 0.0066 7.28 MOPS 25 15 4.53E-02 -6.86E-02
4-CNNB[61] Hematite 0.038 34.00 0.3750 0.3710 0.0043 7.00 MOPS 25 15 -3.12E-01 -4.26E-01
4-CNNB[61] Hematite 0.038 34.00 0.3750 0.3710 0.0042 6.80 MOPSO 25 15 -7.75E-01 -8.89E-01
4-CNNB[61] Hematite 0.038 34.00 0.3750 0.3680 0.0069 6.60 MES 25 15 -1.39E+00 -1.50E+00
4-CNNB[61] Hematite 0.038 34.00 0.3750 0.3750 0.0003 6.10 MES 25 15 -2.77E+00 -2.88E+00
4-CNNB[61] Hematite 0.016 34.00 0.3750 0.3730 0.0024 6.60 MES 25 15 -3.20E+00 -2.95E+00
4-CNNB[61] Hematite 0.024 34.00 0.3750 0.3690 0.0064 6.60 MES 25 15 -2.74E+00 -2.66E+00
4-CNNB[61] Hematite 0.033 34.00 0.3750 0.3680 0.0069 6.60 MES 25 15 -1.39E+00 -1.43E+00
4-CNNB[61] Hematite 0.177 34.00 0.3750 0.3640 0.0110 6.60 MES 25 15 3.58E-01 -4.22E-01
4-CNNB[61] Hematite 0.353 34.00 0.3750 0.3630 0.0120 6.60 MES 25 15 9.97E-01 -8.27E-02
4-CNNB[61] Hematite 0.885 34.00 0.3750 0.3480 0.0270 6.60 MES 25 15 1.34E+00 -1.34E-01
4-CNNB[61] Hematite 1.771 34.00 0.3750 0.3380 0.0370 6.60 MES 25 15 1.78E+00 3.59E-03
4-CNNB[61] Lepidocrocite 0.027 49.00 0.3750 0.3460 0.0290 7.97 HEPES 25 15 1.31E+00 1.20E+00
4-CNNB[61] Lepidocrocite 0.027 49.00 0.3750 0.3610 0.0140 7.67 HEPES 25 15 5.82E-01 4.68E-01
4-CNNB[61] Lepidocrocite 0.027 49.00 0.3750 0.3480 0.0270 7.50 MOPS 25 15 4.92E-02 -6.47E-02
4-CNNB[61] Lepidocrocite 0.027 49.00 0.3750 0.3640 0.0110 7.28 MOPS 25 15 1.62E+00 -4.90E-01
4-CNNB[61] Lepidocrocite 0.027 49.00 0.3750 0.3640 0.0110 7.00 MOPS 25 15 -1.25E+00 -1.36E+00
4-CNNB[61] Lepidocrocite 0.027 49.00 0.3750 0.3620 0.0130 6.80 MOPSO 25 15 -1.74E+00 -1.86E+00
4-CNNB[61] Lepidocrocite 0.027 49.00 0.3750 0.3740 0.0015 6.60 MES 25 15 -2.58E+00 -2.69E+00
4-CNNB[61] Lepidocrocite 0.027 49.00 0.3750 0.3700 0.0046 6.10 MES 25 15 -3.80E+00 -3.92E+00
4-CNNB[61] Lepidocrocite 0.020 49.00 0.3750 0.3740 0.0014 6.60 MES 25 15 -2.58E+00 -2.57E+00
4-CNNB[61] Lepidocrocite 11.980 49.00 0.3750 0.3620 0.0130 6.60 MES 25 15 -5.78E-01 -3.35E+00
4-CNNB[61] Lepidocrocite 0.239 49.00 0.3750 0.3530 0.0220 6.60 MES 25 15 -2.78E-02 -1.10E+00
4-CNNB[61] Lepidocrocite 0.600 49.00 0.3750 0.3190 0.0560 6.60 MES 25 15 3.75E-01 -1.09E+00
4-CNNB[61] Lepidocrocite 1.198 49.00 0.3750 0.2700 0.1050 6.60 MES 25 15 5.05E-01 -1.26E+00
4-CNNB[61] Lepidocrocite 1.798 49.00 0.3750 0.2230 0.1520 6.60 MES 25 15 5.56E-01 -1.39E+00
4-CNNB[61] Lepidocrocite 2.388 49.00 0.3750 0.1820 0.1930 6.60 MES 25 15 5.28E-01 -1.54E+00
4-CNNB[61] Goethite 0.025 51.00 0.3750 0.3440 0.0310 7.97 HEPES 25 15 9.21E-01 8.07E-01
4-CNNB[61] Goethite 0.025 51.00 0.3750 0.3660 0.0094 7.67 HEPES 25 15 3.05E-01 1.91E-01
4-CNNB[61] Goethite 0.025 51.00 0.3750 0.3570 0.0180 7.50 MOPS 25 15 -9.96E-02 -2.14E-01
4-CNNB[61] Goethite 0.025 51.00 0.3750 0.3640 0.0110 7.28 MOPS 25 15 -8.18E-01 -9.32E-01
4-CNNB[61] Goethite 0.025 51.00 0.3750 0.3670 0.0084 7.00 MOPS 25 15 -1.61E+00 -1.73E+00
4-CNNB[61] Goethite 0.025 51.00 0.3750 0.3750 0.0004 6.80 MOPSO 25 15 -1.82E+00 -1.93E+00
4-CNNB[61] Goethite 0.025 51.00 0.3750 0.3730 0.0018 6.60 MES 25 15 -2.26E+00 -2.37E+00
4-CNNB[61] Goethite 0.025 51.00 0.3750 0.3670 0.0076 6.10 MES 25 15 -3.56E+00 -3.67E+00
4-CNNB[61] Goethite 0.020 51.00 0.3750 0.3680 0.0069 6.60 MES 25 15 -2.26E+00 -2.27E+00
4-CNNB[61] Goethite 0.110 51.00 0.3750 0.3660 0.0090 6.60 MES 25 15 -3.19E-01 -1.07E+00
4-CNNB[61] Goethite 0.220 51.00 0.3750 0.3540 0.0210 6.60 MES 25 15 5.00E-01 -5.50E-01
4-CNNB[61] Goethite 0.551 51.00 0.3750 0.3220 0.0530 6.60 MES 25 15 1.03E+00 -4.15E-01
4-CNNB[61] Goethite 1.100 51.00 0.3750 0.2740 0.1010 6.60 MES 25 15 1.46E+00 -2.88E-01
4-CNNB[61] Goethite 1.651 51.00 0.3750 0.2330 0.1420 6.60 MES 25 15 1.66E+00 -2.70E-01
4-CNNB[61] Goethite 2.196 51.00 0.3750 0.1910 0.1840 6.60 MES 25 15 1.83E+00 -2.19E-01
4-CNNB[61] Goethite 0.142 51.00 0.3750 6.60 MES 25 15 1.99E-01 -6.61E-01
4-AcNB[61] Goethite 0.142 51.00 0.3750 6.60 MES 25 15 -6.85E-02 -9.28E-01
4-ClNB[61] Goethite 0.142 51.00 0.3750 6.60 MES 25 15 -5.47E-01 -1.41E+00
4-BrNB[61] Goethite 0.142 51.00 0.3750 6.60 MES 25 15 -5.73E-01 -1.43E+00
NB[61] Goethite 0.142 51.00 0.3750 6.60 MES 25 15 -7.93E-01 -1.65E+00
4-MeNB[61] Goethite 0.142 51.00 0.3750 6.60 MES 25 15 -9.79E-01 -1.84E+00
4-ClNB[62] Goethite 0.040 186.75 1.0000 0.8050 0.1950 7.00 1.05E+00 -3.20E-01
4-ClNB[62] Goethite 7.516 16.10 1.0000 0.9260 0.0740 7.00 1.14E+00 0.00E+00
4-ClNB[62] Ferrihydrite 0.111 252.60 1.0000 0.6650 0.3350 7.00 1.05E+00 -1.56E+00
4-ClNB[62] Lepidocrocite 2.384 60.40 1.0000 0.9250 0.0750 7.00 1.14E+00 -8.60E-01
4-ClNB[63] Goethite 10.000 14.90 1.0000 7.20 HEPES 10 10 - 50 2.26E+00 8.00E-02
4-ClNB[63] Goethite 3.000 14.90 1.0000 7.20 HEPES 10 10 - 50 2.38E+00 7.30E-01
4-ClNB[63] Lepidocrocite 2.700 16.20 1.0000 7.20 HEPES 10 10 - 50 9.20E-01 -7.20E-01
4-ClNB[63] Lepidocrocite 10.000 16.20 1.0000 7.20 HEPES 10 10 - 50 1.03E+00 -1.18E+00
4-ClNB[64] Goethite 0.325 140.00 1.0000 7.00 Bicarbonate 10 100 1.14E+00 -1.79E+00
4-ClNB[64] Goethite 0.325 140.00 1.0000 6.50 Bicarbonate 10 100 1.11E+00 -2.10E+00
NB[65] Goethite 0.500 30.70 0.1000 0.1120 0.0090 6.00 MES 25 12 -1.42E+00 -2.61E+00
NB[65] Goethite 0.500 30.70 0.5000 0.5150 0.0240 6.00 MES 25 15 -7.45E-01 -1.93E+00
NB[65] Goethite 0.500 30.70 1.0000 1.0280 0.0140 6.00 MES 25 19 -7.45E-01 -1.93E+00
NB[65] Goethite 1.000 30.70 0.1000 0.0960 0.0260 6.00 MES 25 13 -1.12E+00 -2.61E+00
NB[65] Goethite 1.000 30.70 0.5000 0.4890 0.0230 6.00 MES 25 14 -5.53E-01 -2.04E+00
NB[65] Goethite 1.000 30.70 1.0000 0.9870 0.0380 6.00 MES 25 19 -2.52E-01 -1.74E+00
NB[65] Goethite 2.000 30.70 0.1000 0.0800 0.0490 6.00 MES 25 11 -8.86E-01 -2.67E+00
NB[65] Goethite 2.000 30.70 0.6000 0.4890 0.0640 6.00 MES 25 14 -1.08E-01 -1.90E+00
NB[65] Goethite 2.000 30.70 1.1000 0.9870 0.0670 6.00 MES 25 14 2.30E-01 -1.56E+00
NB[65] Goethite 4.000 30.70 0.1000 0.0600 0.0650 6.00 MES 25 11 -8.89E-01 -2.98E+00
NB[65] Goethite 4.000 30.70 0.6000 0.3960 0.1550 6.00 MES 25 17 1.43E-01 -1.95E+00
NB[65] Goethite 4.000 30.70 1.0000 0.8360 0.1450 6.00 MES 25 16 4.80E-01 -1.61E+00
NB[65] Goethite 4.000 30.70 5.6000 5.2110 0.3790 6.00 MES 25 15 1.17E+00 -9.19E-01
NB[65] Goethite 1.000 30.70 0.1000 0.0870 0.0300 6.50 MES 25 5.5 -1.74E-01 -1.66E+00
NB[65] Goethite 1.000 30.70 0.5000 0.4920 0.0300 6.50 MES 25 15 3.64E-01 -1.12E+00
NB[65] Goethite 1.000 30.70 1.0000 0.9390 0.0650 6.50 MES 25 18 6.70E-01 -8.17E-01
NB[65] Goethite 2.000 30.70 0.1000 0.0490 0.0730 6.50 MES 25 5.2 3.01E-01 -1.49E+00
NB[65] Goethite 2.000 30.70 0.5000 0.4640 0.0710 6.50 MES 25 14 8.85E-01 -9.03E-01
NB[65] Goethite 2.000 30.70 1.0000 0.9130 0.1280 6.50 MES 25 16 1.12E+00 -6.64E-01
NB[65] Goethite 1.000 30.70 0.1000 0.0630 0.0480 7.00 MOPS 25 5.3 6.12E-01 -8.75E-01
NB[65] Goethite 1.000 30.70 0.5000 0.4690 0.0520 7.00 MOPS 25 9 1.51E+00 2.07E-02
NB[65] Goethite 1.000 30.70 1.0000 0.9360 0.1090 7.00 MOPS 25 18 1.33E+00 -1.53E-01
NB[65] Goethite 2.000 30.70 0.1000 0.0290 0.0880 7.00 MOPS 25 12 6.85E-01 -1.10E+00
NB[65] Goethite 2.000 30.70 0.5000 0.3950 0.1450 7.00 MOPS 25 15 1.59E+00 -1.95E-01
Notes:
a The NACs are Nitrobenzene (NB), 4-chloronitrobenzene(4-ClNB), 4-cyanonitrobenzene (4-CNNB), 4-acetylnitrobenzene (4-AcNB), 4-bromonitrobenzene (4-BrNB), 4-nitrotoluene (4-MeNB). b Initial aqueous Fe(II). c Aqueous Fe(II) after 24h of equilibration. d Difference between b and c. e Initial nominal NAC concentration. f Pseudo-first order rate constant. g Surface area normalized rate constant calculated as kObs / (surface area × mineral loading).

Iron(II) can be complexed by a myriad of organic ligands and may thereby become more reactive towards MCs and other pollutants. The reactivity of an Fe(II)-organic complex depends on the relative preference of the organic ligand for Fe(III) versus Fe(II)[44]. Since the majority of naturally occurring ligands complex Fe(III) more strongly than Fe(II), the reduction potential of the resulting Fe(III) complex is lower than that of aqueous Fe(III); therefore, complexation by organic ligands often renders Fe(II) a stronger reductant thermodynamically[66]. The reactivity of dissolved Fe(II)-organic complexes towards NACs/MCs has been investigated. The intrinsic, second-order rate constants and one electron reduction potentials are listed in Table 2.

In addition to forming organic complexes, iron is ubiquitous in minerals. Iron-bearing minerals play an important role in controlling the environmental fate of contaminants through adsorption[67][68] and reduction[69] processes. Studies have shown that aqueous Fe(II) itself cannot reduce NACs/MCs at circumneutral pH[59][49] but in the presence of an iron oxide (e.g., goethite, hematite, lepidocrocite, ferrihydrite, or magnetite), NACs[61][59][64][60][70] and MCs such as TNT[39], RDX[49], DNAN[54], and NG[50] can be rapidly reduced. Unlike ferric oxides, Fe(II)-bearing minerals including clays[70][71][72][73][74][75][76], green rust[52][53], mackinawite[60][54][58] and pyrite[60][51] do not need aqueous Fe(II) to be reactive toward NACs/MCs. However, upon oxidation, sulfate green rust was converted into lepidocrocite[53], and mackinawite into goethite[58], suggesting that aqueous Fe(II) coupled to Fe(III) oxides might be at least partially responsible for continued degradation of NACs/MCs in the subsurface once the parent reductant (e.g., green rust or iron sulfide) oxidizes.

The reaction conditions and rate constants for a list of studies on MC reduction by iron oxide-aqueous Fe(II) redox couples and by other Fe(II)-containing minerals are shown in Table 3[39][52][49][54][51][55][56]. Unlike hydroquinones and Fe(II) complexes, where second-order rate constants can be readily calculated, the reduction rate constants of NACs/MCs in mineral suspensions are often specific to the experimental conditions used and are usually reported as BET surface area-normalized reduction rate constants (kSA). In the case of iron oxide-Fe(II) redox couples, reduction rate constants have been shown to increase with pH (specifically, with [OH– ]2) and aqueous Fe(II) concentration, both of which correspond to a decrease in the system's reduction potential[61][77][56].

For minerals that contain structural iron(II) and can reduce pollutants in the absence of aqueous Fe(II), the observed rates of reduction increased with increasing structural Fe(II) content, as seen with iron-bearing clays[72][73] and green rust[52]. This dependency on Fe(II) content allows for the derivation of second-order rate constants, as shown on Table 3 for the reduction of RDX by green rust[52], and the development of reduction potential (EH)-based models[72][78][79][80], where EH represents the reduction potential of the iron-bearing clays. Iron-bearing expandable clay minerals represent a special case, which in addition to reduction can remove NACs/MCs through adsorption. This is particularly important for planar NACs/MCs that contain multiple electron-withdrawing nitro groups and can form strong electron donor-acceptor (EDA) complexes with the clay surface[70][74][75].

Although the second-order rate constants derived for Fe(II)-bearing minerals may allow comparison among different studies, they may not reflect changes in reactivity due to variations in surface area, pH, and the presence of ions. Anions such as bicarbonate[52][55][81] and phosphate[52][82] are known to decrease the reactivity of iron oxides-Fe(II) redox couples and green rust. Sulfite has also been shown to decrease the reactivity of hematite-Fe(II) towards the deprotonated form of NTO (Table 3)[56]. Exchanging cations in iron-bearing clays can change the reactivity of these minerals by up to 7-fold[70]. Thus, more comprehensive models are needed to account for the complexities in the subsurface environment.

The reduction of NACs has been widely studied in the presence of different iron minerals, pH, and Fe(II)(aq) concentrations (Table 4)[61][59][64][60][70]. Only selected NACs are included in Table 4. For more information on other NACs and ferruginous reductants, please refer to the cited references.

References

  1. ^ Rosenberry, D. O., Duque, C., and Lee, D. R., 2020. History and Evolution of Seepage Meters for Quantifying Flow between Groundwater and Surface Water: Part 1 – Freshwater Settings. Earth-Science Reviews, 204(103167). doi: 10.1016/j.earscirev.2020.103167.
  2. ^ Duque, C., Russoniello, C. J., and Rosenberry, D. O., 2020. History and Evolution of Seepage Meters for Quantifying Flow between Groundwater and Surface Water: Part 2 – Marine Settings and Submarine Groundwater Discharge. Earth-Science Reviews, 204 ( 103168). doi: 10.1016/j.earscirev.2020.103168.
  3. ^ Constantz, J., 2008. Heat as a Tracer to Determine Streambed Water Exchanges. Water Resources Research, 44 (4).doi: 10.1029/2008WR006996.Open Access Article
  4. ^ Briggs, M. A., Jackson, K. E., Liu, F., Moore, E. M., Bisson, A., Helton, A. M., 2022. Exploring Local Riverbank Sediment Controls on the Occurrence of Preferential Groundwater Discharge Points. Water, 14(1). doi: 10.3390/w14010011  Open Access Article.
  5. ^ Briggs, M. A., Wang, C., Day-Lewis, F. D., Williams, K. H., Dong, W., Lane, J. W., 2019. Return Flows from Beaver Ponds Enhance Floodplain-to-River Metals Exchange in Alluvial Mountain Catchments. Science of the Total Environment, 685, pp. 357–369. doi: 10.1016/j.scitotenv.2019.05.371.  Open Access Manuscript
  6. ^ Mangel, A. R., Dawson, C. B., Rey, D. M., Briggs, M. A., 2022. Drone Applications in Hydrogeophysics: Recent Examples and a Vision for the Future. The Leading Edge, 41 (8), pp. 540–547. doi: 10.1190/tle41080540.
  7. ^ Mwakanyamale, K., Slater, L., Day-Lewis, F., Elwaseif, M., Johnson, C., 2012. Spatially Variable Stage-Driven Groundwater-Surface Water Interaction Inferred from Time-Frequency Analysis of Distributed Temperature Sensing Data. Geophysical Research Letters, 39(6). doi: 10.1029/2011GL050824.  Open Access Article
  8. ^ 8.0 8.1 Slater, L. D., Ntarlagiannis, D., Day-Lewis, F. D., Mwakanyamale, K., Versteeg, R. J., Ward, A., Strickland, C., Johnson, C. D., Lane Jr., J. W., 2010. Use of Electrical Imaging and Distributed Temperature Sensing Methods to Characterize Surface Water-Groundwater Exchange Regulating Uranium Transport at the Hanford 300 Area, Washington. Water Resources Research, 46(10). doi: 10.1029/2010WR009110.  Open Access Article
  9. ^ 9.0 9.1 Selker, J. S., Thévenaz, L., Huwald, H., Mallet, A., Luxemburg, W., van de Giesen, N., Stejskal, M., Zeman, J., Westhoff, M., Parlange, M. B., 2006. Distributed Fiber-Optic Temperature Sensing for Hydrologic Systems. Water Resources Research, 42 (12). doi: 10.1029/2006WR005326.  Open Access Article
  10. ^ 10.0 10.1 Tyler, S. W., Selker, J. S., Hausner, M. B., Hatch, C. E., Torgersen, T., Thodal, C. E., Schladow, S. G., 2009. Environmental Temperature Sensing Using Raman Spectra DTS Fiber-Optic Methods. Water Resources Research, 45(4). doi: 10.1029/2008WR007052.  Open Access Article
  11. ^ Hare, D. K., Briggs, M. A., Rosenberry, D. O., Boutt, D. F., Lane Jr., J. W., 2015. A Comparison of Thermal Infrared to Fiber-Optic Distributed Temperature Sensing for Evaluation of Groundwater Discharge to Surface Water. Journal of Hydrology, 530, pp. 153–166. doi: 10.1016/j.jhydrol.2015.09.059.
  12. ^ 12.0 12.1 Irvine, D. J., Briggs, M. A., Cartwright, I., Scruggs, C. R., Lautz, L. K., 2016. Improved Vertical Streambed Flux Estimation Using Multiple Diurnal Temperature Methods in Series. Groundwater, 55(1), pp. 73-80. doi: 10.1111/gwat.12436.
  13. ^ Koch, F. W., Voytek, E. B., Day-Lewis, F. D., Healy, R., Briggs, M. A., Lane Jr., J. W., Werkema, D., 2016. 1DTempPro V2: New Features for Inferring Groundwater/Surface-Water Exchange. Groundwater, 54(3), pp. 434–439. doi: 10.1111/gwat.12369.
  14. ^ 14.0 14.1 14.2 14.3 Irvine, D. J., Briggs, M. A., Lautz, L. K., Gordon, R. P., McKenzie, J. M., Cartwright, I., 2017. Using Diurnal Temperature Signals to Infer Vertical Groundwater-Surface Water Exchange. Groundwater, 55(1), pp. 10–26. doi: 10.1111/gwat.12459.  Open Access Manuscript
  15. ^ Briggs, M. A., Lautz, L. K., Buckley, S. F., Lane Jr., J. W., 2014. Practical Limitations on the Use of Diurnal Temperature Signals to Quantify Groundwater Upwelling. Journal of Hydrology, 519(B), pp. 1739–1751. doi: 10.1016/j.jhydrol.2014.09.030.
  16. ^ 16.0 16.1 Gordon, R. P., Lautz, L. K., Briggs, M. A., McKenzie, J. M., 2012. Automated Calculation of Vertical Pore-Water Flux from Field Temperature Time Series Using the VFLUX Method and Computer Program. Journal of Hydrology, 420–421, pp. 142–158. doi: 10.1016/j.jhydrol.2011.11.053.
  17. ^ 17.0 17.1 Irvine, D. J., Lautz, L. K., Briggs, M. A., Gordon, R. P., McKenzie, J. M., 2015. Experimental Evaluation of the Applicability of Phase, Amplitude, and Combined Methods to Determine Water Flux and Thermal Diffusivity from Temperature Time Series Using VFLUX 2. Journal of Hydrology, 531(3), pp. 728–737. doi: 10.1016/j.jhydrol.2015.10.054.
  18. ^ Sohn, R. A., Harris, R. N., 2021. Spectral Analysis of Vertical Temperature Profile Time-Series Data in Yellowstone Lake Sediments. Water Resources Research, 57(4), e2020WR028430. doi: 10.1029/2020WR028430.  Open Access Article
  19. ^ Koch, F. W., Voytek, E. B., Day-Lewis, F. D., Healy, R., Briggs, M. A., Werkema, D., Lane Jr., J. W., 2015. 1DTempPro: A Program for Analysis of Vertical One-Dimensional (1D) Temperature Profiles v2.0. U.S. Geological Survey Software Release. doi: 10.5066/F76T0JQS.  Free Download from USGS
  20. ^ 20.0 20.1 20.2 McAliley, W. A., Day-Lewis, F. D., Rey, D., Briggs, M. A., Shapiro, A. M., Werkema, D., 2022. Application of Recursive Estimation to Heat Tracing for Groundwater/Surface-Water Exchange. Water Resources Research, 58(6), e2021WR030443. doi: 10.1029/2021WR030443.  Open Access Article
  21. ^ Cox, M. H., Su, G. W., Constantz, J., 2007. Heat, Chloride, and Specific Conductance as Ground Water Tracers near Streams. Groundwater, 45(2), pp. 187–195. doi: 10.1111/j.1745-6584.2006.00276.x.
  22. ^ 22.0 22.1 22.2 Binley, A., Slater, L., 2020. Resistivity and Induced Polarization: Theory and Applications to the Near-Surface Earth. Cambridge University Press. doi: 10.1017/9781108685955.
  23. ^ Johnson, T. C., Slater, L. D., Ntarlagiannis, D., Day-Lewis, F. D., Elwaseif, M., 2012. Monitoring Groundwater-Surface Water Interaction Using Time-Series and Time- Frequency Analysis of Transient Three-Dimensional Electrical Resistivity Changes. Water Resources Research, 48(7). doi: 10.1029/2012WR011893.  Open Access Article
  24. ^ McLachlan, P., Blanchy, G., Binley, A., 2021. EMagPy: Open-Source Standalone Software for Processing, Forward Modeling and Inversion of Electromagnetic Induction Data. Computers and Geosciences, 146, 104561. doi: 10.1016/j.cageo.2020.104561.
  25. ^ Lane Jr., J. W., Briggs, M. A., Maurya, P. K., White, E. A., Pedersen, J. B., Auken, E., Terry, N., Minsley, B., Kress, W., LeBlanc, D. R., Adams, R., Johnson, C. D., 2020. Characterizing the Diverse Hydrogeology Underlying Rivers and Estuaries Using New Floating Transient Electromagnetic Methodology. Science of the Total Environment, 740, 140074. doi: 10.1016/j.scitotenv.2020.140074.  Open Access Manuscript
  26. ^ d’Ozouville, N., Auken, E., Sorensen, K., Violette, S., de Marsily, G., Deffontaines, B., Merlen, G., 2008. Extensive Perched Aquifer and Structural Implications Revealed by 3D Resistivity Mapping in a Galapagos Volcano. Earth and Planetary Science Letters, 269(3–4), pp. 518–522. doi: 10.1016/j.epsl.2008.03.011.
  27. ^ Day-Lewis, F. D., White, E. A., Johnson, C. D., Lane Jr, J. W., Belaval, M., 2006. Continuous Resistivity Profiling to Delineate Submarine Groundwater Discharge—Examples and Limitations. The Leading Edge, 25(6), pp. 724–728. doi: 10.1190/1.2210056
  28. ^ Cite error: Invalid <ref> tag; no text was provided for refs named Dunnivant1992
  29. ^ Cite error: Invalid <ref> tag; no text was provided for refs named Oh2013
  30. ^ Cite error: Invalid <ref> tag; no text was provided for refs named Oh2009
  31. ^ Cite error: Invalid <ref> tag; no text was provided for refs named Xu2015
  32. ^ Xin, D., 2021. Understanding the Electron Storage Capacity of Pyrogenic Black Carbon: Origin, Redox Reversibility, Spatial Distribution, and Environmental Applications. Doctoral Thesis, University of Delaware. Free download.
  33. ^ Cite error: Invalid <ref> tag; no text was provided for refs named Luan2010
  34. ^ 34.0 34.1 34.2 Cite error: Invalid <ref> tag; no text was provided for refs named Murillo-Gelvez2021
  35. ^ 35.00 35.01 35.02 35.03 35.04 35.05 35.06 35.07 35.08 35.09 35.10 35.11 35.12 35.13 35.14 35.15 35.16 35.17 35.18 35.19 35.20 35.21 35.22 35.23 35.24 35.25 35.26 35.27 35.28 35.29 35.30 35.31 35.32 35.33 35.34 35.35 35.36 35.37 35.38 35.39 35.40 35.41 35.42 35.43 35.44 35.45 35.46 35.47 35.48 35.49 35.50 35.51 35.52 35.53 35.54 35.55 Cite error: Invalid <ref> tag; no text was provided for refs named Schwarzenbach1990
  36. ^ 36.00 36.01 36.02 36.03 36.04 36.05 36.06 36.07 36.08 36.09 36.10 36.11 36.12 36.13 36.14 36.15 36.16 Cite error: Invalid <ref> tag; no text was provided for refs named Murillo-Gelvez2019
  37. ^ 37.0 37.1 37.2 37.3 37.4 37.5 Cite error: Invalid <ref> tag; no text was provided for refs named Hartenbach2008
  38. ^ 38.0 38.1 38.2 38.3 38.4 38.5 38.6 Cite error: Invalid <ref> tag; no text was provided for refs named Schwarzenbach2016
  39. ^ 39.00 39.01 39.02 39.03 39.04 39.05 39.06 39.07 39.08 39.09 39.10 39.11 39.12 39.13 39.14 39.15 39.16 39.17 39.18 39.19 Cite error: Invalid <ref> tag; no text was provided for refs named Hofstetter1999
  40. ^ Cite error: Invalid <ref> tag; no text was provided for refs named Kwon2008
  41. ^ Riefler, R.G., and Smets, B.F., 2000. Enzymatic Reduction of 2,4,6-Trinitrotoluene and Related Nitroarenes: Kinetics Linked to One-Electron Redox Potentials. Environmental Science and Technology, 34(18), pp. 3900–3906. DOI: 10.1021/es991422f
  42. ^ 42.00 42.01 42.02 42.03 42.04 42.05 42.06 42.07 42.08 42.09 42.10 42.11 Salter-Blanc, A.J., Bylaska, E.J., Johnston, H.J., and Tratnyek, P.G., 2015. Predicting Reduction Rates of Energetic Nitroaromatic Compounds Using Calculated One-Electron Reduction Potentials. Environmental Science and Technology, 49(6), pp. 3778–3786. DOI: 10.1021/es505092s   Open access article.
  43. ^ 43.0 43.1 Cite error: Invalid <ref> tag; no text was provided for refs named Naka2008
  44. ^ 44.0 44.1 44.2 Cite error: Invalid <ref> tag; no text was provided for refs named Kim2009
  45. ^ 45.00 45.01 45.02 45.03 45.04 45.05 45.06 45.07 45.08 45.09 45.10 Gao, Y., Zhong, S., Torralba-Sanchez, T.L., Tratnyek, P.G., Weber, E.J., Chen, Y., and Zhang, H., 2021. Quantitative structure activity relationships (QSARs) and machine learning models for abiotic reduction of organic compounds by an aqueous Fe(II) complex. Water Research, 192, p. 116843. DOI: 10.1016/j.watres.2021.116843
  46. ^ Cite error: Invalid <ref> tag; no text was provided for refs named Naka2006
  47. ^ 47.0 47.1 47.2 47.3 Uchimiya, M., Gorb, L., Isayev, O., Qasim, M.M., and Leszczynski, J., 2010. One-electron standard reduction potentials of nitroaromatic and cyclic nitramine explosives. Environmental Pollution, 158(10), pp. 3048–3053. DOI: 10.1016/j.envpol.2010.06.033
  48. ^ Cite error: Invalid <ref> tag; no text was provided for refs named Kim2007
  49. ^ 49.00 49.01 49.02 49.03 49.04 49.05 49.06 49.07 49.08 49.09 49.10 49.11 49.12 49.13 49.14 49.15 Gregory, K.B., Larese-Casanova, P., Parkin, G.F., and Scherer, M.M., 2004. Abiotic Transformation of Hexahydro-1,3,5-trinitro-1,3,5-triazine by FeII Bound to Magnetite. Environmental Science and Technology, 38(5), pp. 1408–1414. DOI: 10.1021/es034588w
  50. ^ 50.0 50.1 Oh, S.-Y., Cha, D.K., Kim, B.J., and Chiu, P.C., 2004. Reduction of Nitroglycerin with Elemental Iron: Pathway, Kinetics, and Mechanisms. Environmental Science and Technology, 38(13), pp. 3723–3730. DOI: 10.1021/es0354667
  51. ^ 51.0 51.1 51.2 51.3 51.4 Oh, S.-Y., Chiu, P.C., and Cha, D.K., 2008. Reductive transformation of 2,4,6-trinitrotoluene, hexahydro-1,3,5-trinitro-1,3,5-triazine, and nitroglycerin by pyrite and magnetite. Journal of hazardous materials, 158(2-3), pp. 652–655. DOI: 10.1016/j.jhazmat.2008.01.078
  52. ^ 52.0 52.1 52.2 52.3 52.4 52.5 52.6 52.7 Cite error: Invalid <ref> tag; no text was provided for refs named Larese-Casanova2008
  53. ^ 53.0 53.1 53.2 53.3 Khatiwada, R., Root, R.A., Abrell, L., Sierra-Alvarez, R., Field, J.A., and Chorover, J., 2018. Abiotic reduction of insensitive munition compounds by sulfate green rust. Environmental Chemistry, 15(5), pp. 259–266. DOI: 10.1071/EN17221
  54. ^ 54.0 54.1 54.2 54.3 54.4 54.5 Berens, M.J., Ulrich, B.A., Strehlau, J.H., Hofstetter, T.B., and Arnold, W.A., 2019. Mineral identity, natural organic matter, and repeated contaminant exposures do not affect the carbon and nitrogen isotope fractionation of 2,4-dinitroanisole during abiotic reduction. Environmental Science: Processes and Impacts, 21(1), pp. 51-62. DOI: 10.1039/C8EM00381E
  55. ^ 55.0 55.1 55.2 55.3 55.4 Strehlau, J.H., Berens, M.J., and Arnold, W.A., 2018. Mineralogy and buffer identity effects on RDX kinetics and intermediates during reaction with natural and synthetic magnetite. Chemosphere, 213, pp. 602–609. DOI: 10.1016/j.chemosphere.2018.09.139
  56. ^ 56.00 56.01 56.02 56.03 56.04 56.05 56.06 56.07 56.08 56.09 56.10 Cárdenas-Hernandez, P.A., Anderson, K.A., Murillo-Gelvez, J., di Toro, D.M., Allen, H.E., Carbonaro, R.F., and Chiu, P.C., 2020. Reduction of 3-Nitro-1,2,4-Triazol-5-One (NTO) by the Hematite–Aqueous Fe(II) Redox Couple. Environmental Science and Technology, 54(19), pp. 12191–12201. DOI: 10.1021/acs.est.0c03872
  57. ^ 57.00 57.01 57.02 57.03 57.04 57.05 57.06 57.07 57.08 57.09 57.10 57.11 57.12 57.13 57.14 Cite error: Invalid <ref> tag; no text was provided for refs named Tong2021
  58. ^ 58.0 58.1 58.2 58.3 58.4 58.5 58.6 58.7 58.8 58.9 Menezes, O., Yu, Y., Root, R.A., Gavazza, S., Chorover, J., Sierra-Alvarez, R., and Field, J.A., 2021. Iron(II) monosulfide (FeS) minerals reductively transform the insensitive munitions compounds 2,4-dinitroanisole (DNAN) and 3-nitro-1,2,4-triazol-5-one (NTO). Chemosphere, 285, p. 131409. DOI: 10.1016/j.chemosphere.2021.131409
  59. ^ 59.0 59.1 59.2 59.3 59.4 Cite error: Invalid <ref> tag; no text was provided for refs named Klausen1995
  60. ^ 60.0 60.1 60.2 60.3 60.4 60.5 60.6 Cite error: Invalid <ref> tag; no text was provided for refs named Elsner2004
  61. ^ 61.00 61.01 61.02 61.03 61.04 61.05 61.06 61.07 61.08 61.09 61.10 61.11 61.12 61.13 61.14 61.15 61.16 61.17 61.18 61.19 61.20 61.21 61.22 61.23 61.24 61.25 61.26 61.27 61.28 61.29 61.30 61.31 61.32 61.33 61.34 61.35 61.36 61.37 61.38 61.39 61.40 61.41 61.42 61.43 61.44 61.45 61.46 61.47 61.48 61.49 61.50 61.51 61.52 61.53 61.54 61.55 61.56 61.57 61.58 61.59 61.60 61.61 61.62 61.63 61.64 61.65 61.66 61.67 Cite error: Invalid <ref> tag; no text was provided for refs named Colón2006
  62. ^ 62.0 62.1 62.2 62.3 Cite error: Invalid <ref> tag; no text was provided for refs named Jones2016
  63. ^ 63.0 63.1 63.2 63.3 Cite error: Invalid <ref> tag; no text was provided for refs named Fan2016
  64. ^ 64.0 64.1 64.2 64.3 Cite error: Invalid <ref> tag; no text was provided for refs named Strehlau2016
  65. ^ 65.00 65.01 65.02 65.03 65.04 65.05 65.06 65.07 65.08 65.09 65.10 65.11 65.12 65.13 65.14 65.15 65.16 65.17 65.18 65.19 65.20 65.21 65.22 65.23 Cite error: Invalid <ref> tag; no text was provided for refs named Stewart2018
  66. ^ Strathmann, T.J., 2011. Redox Reactivity of Organically Complexed Iron(II) Species with Aquatic Contaminants. Aquatic Redox Chemistry, American Chemical Society,1071(14), pp. 283-313. DOI: 10.1021/bk-2011-1071.ch014
  67. ^ Linker, B.R., Khatiwada, R., Perdrial, N., Abrell, L., Sierra-Alvarez, R., Field, J.A., and Chorover, J., 2015. Adsorption of novel insensitive munitions compounds at clay mineral and metal oxide surfaces. Environmental Chemistry, 12(1), pp. 74–84. DOI: 10.1071/EN14065
  68. ^ Jenness, G.R., Giles, S.A., and Shukla, M.K., 2020. Thermodynamic Adsorption States of TNT and DNAN on Corundum and Hematite. The Journal of Physical Chemistry C, 124(25), pp. 13837–13844. DOI: 10.1021/acs.jpcc.0c04512
  69. ^ Gorski, C.A., and Scherer, M.M., 2011. Fe2+ Sorption at the Fe Oxide-Water Interface: A Revised Conceptual Framework. Aquatic Redox Chemistry, American Chemical Society, 1071(15), pp. 315–343. DOI: 10.1021/bk-2011-1071.ch015
  70. ^ 70.0 70.1 70.2 70.3 70.4 Cite error: Invalid <ref> tag; no text was provided for refs named Hofstetter2006
  71. ^ Cite error: Invalid <ref> tag; no text was provided for refs named Schultz2000
  72. ^ 72.0 72.1 72.2 Cite error: Invalid <ref> tag; no text was provided for refs named Luan2015a
  73. ^ 73.0 73.1 Cite error: Invalid <ref> tag; no text was provided for refs named Luan2015b
  74. ^ 74.0 74.1 Cite error: Invalid <ref> tag; no text was provided for refs named Hofstetter2003
  75. ^ 75.0 75.1 Cite error: Invalid <ref> tag; no text was provided for refs named Neumann2008
  76. ^ Cite error: Invalid <ref> tag; no text was provided for refs named Hofstetter2008
  77. ^ Cite error: Invalid <ref> tag; no text was provided for refs named Gorski2016
  78. ^ Gorski, C.A., Aeschbacher, M., Soltermann, D., Voegelin, A., Baeyens, B., Marques Fernandes, M., Hofstetter, T.B., and Sander, M., 2012. Redox Properties of Structural Fe in Clay Minerals. 1. Electrochemical Quantification of Electron-Donating and -Accepting Capacities of Smectites. Environmental Science and Technology, 46(17), pp. 9360–9368. DOI: 10.1021/es3020138
  79. ^ Gorski, C.A., Klüpfel, L., Voegelin, A., Sander, M., and Hofstetter, T.B., 2012. Redox Properties of Structural Fe in Clay Minerals. 2. Electrochemical and Spectroscopic Characterization of Electron Transfer Irreversibility in Ferruginous Smectite, SWa-1. Environmental Science and Technology, 46(17), pp. 9369–9377. DOI: 10.1021/es302014u
  80. ^ Gorski, C.A., Klüpfel, L.E., Voegelin, A., Sander, M. and Hofstetter, T.B., 2013. Redox Properties of Structural Fe in Clay Minerals: 3. Relationships between Smectite Redox and Structural Properties. Environmental Science and Technology, 47(23), pp. 13477–13485. DOI: 10.1021/es403824x
  81. ^ Chen, G., Hofstetter, T.B., and Gorski, C.A., 2020. Role of Carbonate in Thermodynamic Relationships Describing Pollutant Reduction Kinetics by Iron Oxide-Bound Fe2+. Environmental Science and Technology, 54(16), pp. 10109–10117. DOI: 10.1021/acs.est.0c02959
  82. ^ Bocher, F., Géhin, A., Ruby, C., Ghanbaja, J., Abdelmoula, M., and Génin, J.M.R., 2004. Coprecipitation of Fe(II–III) hydroxycarbonate green rust stabilised by phosphate adsorption. Solid State Sciences, 6(1), pp. 117–124. DOI: 10.1016/j.solidstatesciences.2003.10.004

See Also

Retrieved from "https://www.enviro.wiki/index.php?title=User:Jhurley/sandbox&oldid=16201"