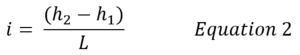Difference between revisions of "User:Debra Tabron/sandbox"

From Enviro Wiki
Jump to: navigation, search
Line 1: Line 1:
−
Nonionic and nonpolar organic contaminants including chlorinated solvents and petroleum hydrocarbons can become associated with solid phase organic matter in the soil, sediment, and rock, slowing contaminant migration in groundwater and reducing the efficacy of many remedial technologies.  When amorphous organic matter is the primary sorbent, sorption is linear and distribution coefficients can be estimated from empirical correlations with contaminant properties (aqueous solubility or octanol-water partition coefficient) and site specific measurements of solid phase organic carbon.  However, when thermally altered carbonaceous materials (TACMs) are present, sorption may be non-linear and the empirical correlations may substantially underestimate sorption at low contaminant concentrations.
+
 
  
 
<div style="float:right;margin:0 0 2em 2em;">__TOC__</div>
 
<div style="float:right;margin:0 0 2em 2em;">__TOC__</div>
  
 
'''Related Article(s):'''
 
'''Related Article(s):'''
−
*[[Chlorinated Solvents]]
+
*[[Direct Push (DP) Technology]]
−
*[[Petroleum Hydrocarbons]]
+
*[[Geophysical Methods]]
  
  
−
'''CONTRIBUTOR(S):''' [[Richelle Allen-King]]
+
'''CONTRIBUTOR(S):''' [[Gaisheng Liu]] and [[Jim Butler]]
  
 
'''Key Resource(s)''':
 
'''Key Resource(s)''':
−
*[[media:1990-Piwoni-Basic_concepts_sorption_haz_site_EPA_540-4-90-053.pdf| Basic Concepts of Contaminant Sorption at Hazardous Waste Sites]]<ref>Piwoni, M.D. and Keeley, J.W., 1990. Basic concepts of contaminant sorption at hazardous waste sites. Ground-Water Issue; EPA-540/4-90/053. [[media:1990-Piwoni-Basic_concepts_sorption_haz_site_EPA_540-4-90-053.pdf| Report.pdf]]</ref>
+
*[https://doi.org/10.1007/1-4020-3102-5_2 Hydrogeological Methods for Estimation of Spatial Variations in Hydraulic Conductivity]<ref name= "Butler2005">Butler, J.J., 2005. Hydrogeological methods for estimation of spatial variations in hydraulic conductivity. In Hydrogeophysics (pp. 23-58). Springer, Dordrecht. [https://doi.org/10.1007/1-4020-3102-5_2 doi: 10.1007/1-4020-3102-5_2 ]</ref>
 +
*Hydraulic conductivity profiling with direct push methods<ref name= "Liu2012"> Liu, G., Butler, J.J., Reboulet, E. and Knobbe, S., 2012. Hydraulic conductivity profiling with direct push methods. Grundwasser, 17(1), pp.19-29. [https://doi.org/10.1007/s00767-011-0182-9 doi: 10.1007/s00767-011-0182-9]</ref>
 +
*Groundwater<ref name= "Freeze1979">Freeze, R.A., Cherry, J.A. and Groundwater., A., 1979. Prentice-Hall. Inc., Englewood Cliffs, NJ ISBN 0-13-365312-9.</ref>
  
 
==Introduction==
 
==Introduction==
−
Sorption is a non-mechanistic term that describes uptake of a contaminant by a solid phase sorbent (soil, sediment, rock or an engineered material such as [https://en.wikipedia.org/wiki/Activated_carbon activated carbon]).  This article focuses on sorption of nonionic and nonpolar organic contaminants and their associations with subsurface materials.  For these contaminants, sorption is almost exclusively associated with organic matter in the solids and is a reversible process. Sorption of ionic and polar organic contaminants is not described in this article.
+
Hydraulic conductivity is mathematically defined as the parameter ''K'' in Darcy’s Law<ref>Darcy, H. (1856). Les Fontaines Publiques de la Ville de Dijon, Dalmont, Paris. [https://doi.org/10.1029/2001wr000727 doi: 10.1029/2001WR000727]</ref> (see Fig. 1),
−
 
 
−
In this article, the term ‘sorption’ includes all processes that cause the dissolved organic compound (sorbate) to become associated with the solid phase (sorbent). For nonpolar organic compounds, sorption occurs by either adsorption or absorption. [https://en.wikipedia.org/wiki/Absorption_(chemistry) Absorption] is a volume-based process whereby the sorbate diffuses into the organic matter, analogous to the way that organic contaminants partition between immiscible oil and aqueous phases. In contrast, [https://en.wikipedia.org/wiki/Adsorption adsorption] describes the interaction between the contaminant and the sorbent surfaces.
 
−
 
 
−
==Measuring Sorption==
 
−
[[File:Allen-King1w2 Fig1a.png|right|thumb| 400 px|Figure 1a. Batch reactor experiments to generate points on a sorption isotherm (Fig. 1b). This Figure shows two samples prepared in duplicate with soil-free control vials and vials to verify the contaminant mass added to the systems<ref name= "Chiou1983">Chiou, C.T., Porter, P.E. and Schmedding, D.W., 1983. Partition equilibriums of nonionic organic compounds between soil organic matter and water. Environmental Science & Technology, 17(4), pp.227-231. [http://dx.doi.org/10.1021/es00110a009 doi: 10.1021/es00110a009]</ref>.]][[File:Allen-King1w2 Fig1b.png|thumb|400 px|Figure 1b. Linear isotherms for eight compounds in one soil<ref name= "Chiou1983"/>. ]]
 
  
−
Sorption can be measured in the laboratory by placing a known mass of the contaminant, water, and uncontaminated sediment in a batch reactor (Fig. 1a). The system is mixed for a specific duration (contact time) and then the aqueous and sorbed contaminant concentrations are determined. This process is repeated, adding a range of different initial contaminant masses to achieve a range of aqueous contaminant concentrations. When the experiment is run at constant temperature until the concentrations in the solid and liquid phases approach equilibrium, the resulting data plot is termed an isotherm. Figure 1b shows linear sorption isotherms for eight compounds measured in one soil.  
+
[[File:Liu1w2 Eq1.png|300 px]]
  
−
The time required to reach equilibrium can vary depending on the contaminant and sorbent.  In studies with aquifer material from Canadian Forces Base Borden, tetrachloroethene (PCE) sorption reached equilibrium within 2 - 4 weeks, but tetrachlorobenzene did not reach equilibrium after 100 days. Powdered (pulverized) samples equilibrated more quickly indicating mass transfer within the grains was limiting<ref>Ball, W.P. and Roberts, P.V., 1991. Long-term sorption of halogenated organic chemicals by aquifer material. 2. Intraparticle diffusion. Environmental Science & Technology, 25(7), pp.1237-1249. [http://dx.doi.org/10.1021/es00019a003 doi:10.1021/es00019a003]</ref>.
+
{|
 +
|-
 +
| where:
 +
|-
 +
| ''Q'' || is the flow rate across area ''A'' of a porous medium,
 +
|-
 +
| ''K'' || is the hydraulic conductivity, and
 +
|-
 +
| ''i'' || is the hydraulic gradient, which can be computed as:
 +
|}
  
−
In some cases, the experimental data show an approximately linear relationship between aqueous and sorbed concentration, and the experimental results can be summarized in the form of a partition or distribution coefficient, ''K<sub>d</sub>'': </br>
+
[[File:Liu1w2 Eq2.png| 300 px]]
  
−
[[File:Allen-King1w2 Eq1.png|400 px]]
+
{|
 +
|-
 +
| where:
 +
|-
 +
| ''h<sub>1</sub>'' and ''h<sub>2</sub>''  &nbsp; &nbsp; || are the hydraulic heads at the ends of the experimental domain, and
 +
|-
 +
| ''L'' || is the total length.
 +
|}
  
−
where ''C<sub>S</sub>'' is the solid (sorbed) concentration and ''C<sub>w<sub>'' is the aqueous (dissolved) concentration. By convention, ''C<sub>s</sub>'' has units of µg/g and ''C<sub>s</sub>'' has units of µg/mL, so ''K<sub>d</sub>'' has units of mL/g.
+
[[File:Liu1w2 Fig1.png|thumb|Figure 1. Schematic of Darcy’s Law flow experiment.]]
  
−
When the relationship between ''C<sub>s</sub>'' and ''C<sub>w</sub>'' is non-linear, the experimental data are commonly represented by the Freundlich isotherm equation:</br>
+
Hydraulic conductivity is dependent on the properties of both water and the porous medium,
−
[[File:Allen-King1w2 Eq2.png|400px]]
 
  
−
where K''<sub>F</sub>'' and ''n'' are empirically estimated coefficients specific to the sorbate, sorbent and equation used.
+
[[File:Liu1w2 Eq3.png|300 px]]
  
−
In most cases, ''absorption'' processes follow a linear isotherm.  However, ''adsorption'' processes often follow a nonlinear relationship between the sorbed and dissolved contaminant concentrations.  When both absorption and adsorption occur, a non-linear relationship is used to represent the sorption results.  
+
{|
 +
|-
 +
| where:
 +
|-
 +
| ''k'' || is the intrinsic permeability of the medium, a parameter which is solely dependent on the geometry of the interconnected pores,
 +
|-
 +
| ''g'' || is the gravitational constant,
 +
|-
 +
| ''&rho;'' || is the density of the pore water, and
 +
|-
 +
| ''&mu;'' || is the dynamic viscosity of the pore water, respectively.
 +
|}
  
−
==Impact on Groundwater Transport==
+
Many approaches have been developed to characterize ''K''<ref name= "Butler2005"/>. These approaches can be grouped into two general categories based on how the ''K'' estimates are obtained:
−
Sorption reduces the amount of contaminant in the aqueous phase, slowing contaminant migration. Sorbed contaminants are also less available for biological or chemical degradation reactions, which will reduce the effectiveness of many remedial technologies.
 
  
−
The average rate that a contaminant migrates in groundwater is reduced because the sorbed portion of the contaminant does not migrate.  The impact of sorption on the average contaminant transport velocity can be estimated using a Retardation Factor (''R''):
+
*hydraulic methods that involve water injection or extraction and the measurement of the induced pressure response, and
 +
* indirect methods that rely on empirical correlations, often site-specific in nature, between ''K'' and other more readily evaluated formation properties (e.g., resistance to electric current).
  
 +
Because hydraulic methods can be directly related to the mathematical definition of ''K'' through Darcy’s Law, ''K'' estimates obtained with those methods are generally considered to be more reliable than those obtained with indirect methods.
  
−
[[File:Allen-King1w2 Eq3.png|600 px]]
+
Other classifications of ''K'' characterization approaches are possible. For example, approaches can be divided into those based on data collected in the field and those based on measurements on core samples in the laboratory. In the latter case, there can be considerable uncertainty about how representative the core sample is of field conditions.  
  
 +
Field-based approaches can be further subdivided based on whether the measurement is conducted in the subsurface or on the surface. Subsurface measurements provide the most reliable information about ''K'' variations at the scale needed for environmental site investigations. Nearly all field-based hydraulic methods are performed in the subsurface and require either boreholes or direct push (DP) installations for extracting or injecting water and monitoring the induced head changes. Compared to methods that rely on existing wells, DP approaches can be applied essentially wherever ''K'' information is needed, thus greatly expanding the spatial coverage of ''K'' measurement in the field. DP approaches, however, are generally limited to use in relatively shallow (20-30 m from land surface) unconsolidated settings.
  
−
[[File:Allen-King1w2 Fig2.png|thumb|400 px|Figure 2. Effect of Freundlich ''n'' on ''R''.]]
+
Field ''K'' measurements can also be performed on the land surface or in an aircraft. Most of these are geophysical approaches that involve measuring electrical, magnetic, or seismic properties of the formation and then transforming them into ''K'' estimates using empirical relations. The biggest advantage of surface or airborne approaches is their minimal site disturbance, as no subsurface boring is needed. However, the resolution that can be provided is limited, as the measurements are typically affected by conditions over a relatively large volume of the formation. Geophysical methods can also be performed in boreholes. Borehole geophysical methods can provide a much higher resolution description of ''K'' than surface-based methods.
−
Figure 2 illustrates the effect of ''C<sub>w</sub>'' on ''R'' when 1/''n'' is less than 1 and ρ_b ''&rho;<sub>b</sub>'' = 1.5 g/cm<sup>3</sup>'', θ_w ''&theta;<sub>w</sub>'' = 0.3 mL/cm<sup>3</sup> and ''K<sub>F</sub>'' = 2. When 1/''n'' is less than 1, sorption has limited effect in slowing the migration of a high concentration plume (''C<sub>w</sub>'' > 10 mg/L). However, as the aquifer is remediated and contaminant concentrations drop below 0.1 mg/L, non-linear sorption has a much more pronounced impact, slowing aquifer cleanup.
 
−
 
 
−
[[File:Allen-King1w2 Fig3.png|thumb|400 px|Figure 3. Linear correlation between organic carbon content (''f<sub>oc</sub>'') and sorption distribution coefficient (<sub>Kd</sub>) for four chlorinated aromatic contaminants<ref name= "Schwarzenbach1981"/>. ]]
 
−
 
 
−
When sorption of the contaminant is described by a linear isotherm and sorption processes are fast relative to water flow, ''R'' can be estimated as:
 
−
 
 
−
[[File:Allen-King1w2 Eq4.png|400 px]]
 
 
   
 
   
−
where ρ_b ''&rho;<sub>b</sub>'' is the bulk density of the solid phase and θ_w ''&theta;<sub>w</sub>'' is the water filled porosity. When sorption is non-linear and is described with the Freundlich isotherm equation, ''R'' can be estimated as:
+
The scale of measurement is an important factor to consider when assessing various approaches. For water-supply investigations, a single estimate of ''K'' averaged over a large volume of an aquifer will usually suffice; such an estimate is commonly obtained via pumping tests in a well<ref name= "Freeze1979"/>. For water-quality investigations, however, ''K'' estimates over a large measurement volume are often of limited value<ref name= "Butler2009">Butler Jr, J.J., 2009. Pumping tests for aquifer evaluation - Time for a change?. Groundwater, 47(5), pp.615-617. [https://doi.org/10.1111/j.1745-6584.2008.00488.x doi: 10.1111/j.1745-6584.2008.00488.x]</ref>. In that case, small-scale ''K'' measurements that provide information about local geological controls on groundwater flow and transport are usually required to obtain reliable predictions of contaminant behavior and to design effective remediation systems.
  
−
[[File:Allen-King1w2 Eq5.png|400px]]
+
In this article, we focus on the approaches that can be used to obtain small-scale, localized measurements of ''K'' for environmental site investigations. Only the more commonly used approaches are discussed. Some other approaches, such as dipole flow tests<ref>Kabala, Z.J., 1993. The dipole flow test: A new single‐borehole test for aquifer characterization. Water Resources Research, 29(1), pp.99-107. [https://doi.org/10.1029/92WR01820 doi: 10.1029/92WR01820]</ref><ref>Zlotnik, V.A. and Zurbuchen, B.R., 1998. Dipole probe: Design and field applications of a single‐borehole device for measurements of vertical variations of hydraulic conductivity. Groundwater, 36(6), pp.884-893. [https://doi.org/10.1111/j.1745-6584.1998.tb02095.x doi: 10.1111/j.1745-6584.1998.tb02095.x]</ref>, tracer tests<ref>Datta‐Gupta, A., Yoon, S., Vasco, D.W. and Pope, G.A., 2002. Inverse modeling of partitioning interwell tracer tests: A streamline approach. Water Resources Research, 38(6), pp.15-1. [https://doi.org/10.1029/2001WR000597 doi: 10.1029/2001WR000597]</ref>, or hydraulic tomography<ref>Yeh, T.C.J. and Liu, S., 2000. Hydraulic tomography: Development of a new aquifer test method. Water Resources Research, 36(8), pp.2095-2105. [[media:2000-Yeh-Hydraulic_Tomography..Development_of_a_new_aquifer_test_method.pdf| Report.pdf]]</ref><ref>Bohling, G.C. and Butler Jr, J.J., 2010. Inherent limitations of hydraulic tomography. Groundwater, 48(6), pp.809-824. [https://doi.org/10.1111/j.1745-6584.2010.00757.x doi: 10.1111/j.1745-6584.2010.00757.x]</ref> will not be discussed here. 
  
−
==''K<sub>d</sub>'' Estimation Methods==
+
==Hydraulic Testing Approaches==
−
Multiple studies<ref name= "Schwarzenbach1981">Schwarzenbach, R.P. and Westall, J., 1981. Transport of nonpolar organic compounds from surface water to groundwater. Laboratory sorption studies. Environmental Science & Technology, 15(11), pp.1360-1367. [http://dx.doi.org/10.1021/es00093a009  doi: 10.1021/es00093a009]</ref><ref>Karickhoff, S.W., 1981. Semi-empirical estimation of sorption of hydrophobic pollutants on natural sediments and soils. Chemosphere, 10(8), pp.833-846. [http://dx.doi.org/10.1016/0045-6535(81)90083-7 doi:10.1016/0045-6535(81)90083-7]</ref><ref>Chiou, C.T., Peters, L.J. and Freed, V.H., 1979. A physical concept of soil-water equilibria for nonionic organic compounds. Science, 206(4420), pp.831-832. [https://doi.org/10.1126/science.206.4420.831 doi: 10.1126/science.206.4420.831]</ref> showed that sorption of nonpolar organic contaminants is typically proportional to the organic carbon content of the solid phase (Fig. 3).  When this occurs, an organic carbon normalized partitioning coefficient, ''K<sub>oc</sub>'', is used:
 
  
−
[[File:Allen-King1w2 Eq6.png|300 px]]
+
===Pumping Tests===
 +
The pumping test is the most common method for determining ''K'' over a relatively large volume of an aquifer in water-supply investigations<ref name= "Butler2009"/>. During a typical test, the pumping rate is kept constant, although it can be varied in time to obtain better signal-to-noise ratios in the acquired data<ref>Rasmussen, T.C., Haborak, K.G. and Young, M.H., 2003. Estimating aquifer hydraulic properties using sinusoidal pumping at the Savannah River site, South Carolina, USA. Hydrogeology Journal, 11(4), pp.466-482. [https://doi.org/10.1007/s10040-003-0255-7 doi: 10.1007/s10040-003-0255-7]</ref>. In the constant-rate approach, a well, preferably centrally located at the site, is pumped while induced head changes are monitored at that and nearby wells. The head changes, along with the pumping rate, can then be used to estimate aquifer parameters using different models of the well-aquifer configuration<ref>Batu, V., 1998. Aquifer hydraulics: a comprehensive guide to hydrogeologic data analysis. John Wiley & Sons.</ref><ref>Kruseman, G.P., De Ridder, N.A. and Verweij, J.M., 1990. Analysis and evaluation of pumping test data – ILRI Pub. 47. The Netherlands: International institute for land reclamation and improvement</ref>. Pumping test analyses can be facilitated using software packages like AQTESOLV (Aquifer Test Solver), which has been developed for analyzing different types of aquifer tests<ref name= "Duffield2007">Duffield, G.M., 2007. AQTESOLV for Windows Version 4.5 User's Guide. HydroSOLVE, Reston, VA.</ref>.
  
−
where ''f<sub>oc</sub>'' is the fractional organic carbon content of the soil, sediment or rock. This approach empirically separates variations in ''K<sub>d</sub>'' according to variations in the organic matter concentration, an important property of the sorbent, and the ''K<sub>oc</sub>'', which is intended to capture differences in the chemical properties of the contaminant.  
+
Pumping tests are primarily performed to obtain large-scale volumetric averages of aquifer parameters as well as information about aquifer boundaries. However, one form of the pumping test, the step-drawdown test, is specifically directed at getting information about the efficiency of the pumping well. The ''K'' estimate from a pumping test is an average over a large volume of the formation and does not provide information at the scale of most relevance for issues involving contaminant transport (e.g., meters or less). Thus, pumping tests are less commonly employed for environmental site investigations<ref name= "Butler2009"/>.  
  
−
Experimental investigations (summarized in Allen-King et al., 2002<ref name= "Allenking2002">Allen-King, R.M., Grathwohl, P. and Ball, W.P., 2002. New modeling paradigms for the sorption of hydrophobic organic chemicals to heterogeneous carbonaceous matter in soils, sediments, and rocks. Advances in Water Resources, 25(8), pp.985-1016. [http://dx.doi.org/10.1016/S0309-1708(02)00045-3 doi: 10.1016/S0309-1708(02)00045-3]</ref>) with a variety of sorbents and contaminants has shown that ''K<sub>oc</sub>'' values are correlated with contaminant hydrophobicity. This allows ''K<sub>oc</sub>'' to be estimated using empirical correlations with the contaminant aqueous solubility or [https://en.wikipedia.org/wiki/Partition_coefficient octanol-water partition coefficient] (''K<sub>ow</sub>'') (Fig. 4). Using this approach, ''K<sub>d</sub>'' can be estimated using site specific measurements of ''f<sub>oc</sub>'' and literature values of contaminant properties. 
+
===Slug Tests===
−
[[File:Allen-King1w2 Fig4.png|thumb|center|500 px| Figure 4. Empirical correlations between log ''K<sub>oc</sub>''  and log ''K<sub>ow</sub>''. Variations arise because the studies used different contaminant compounds and different field samples. Figure from Allen-King et al., 2002<ref name= "Allenking2002"/>, which also lists the correlation equations.]]
+
The slug test is one of the most common methods for determining ''K'' at the scale of relevance for environmental site investigations<ref name= "Butler1997">Butler Jr, J.J., 1997. The design, performance, and analysis of slug tests. Crc Press.</ref><ref name= "Butler2009"/>. Slug tests are typically performed in existing wells at multiple horizontal and vertical locations across the site to characterize the spatial distribution of ''K'' values. However, slug tests can also be performed in temporary installations such as DP rods. In this approach, a near-instantaneous head change is applied in the well or DP rods and the subsequent head recovery is used to estimate ''K''. The initial head change can be introduced using a solid object (slug), compressed gas (pneumatic system), or by the addition/removal of a certain amount of water<ref name= "Butler1997"/>. The recovery data can be analyzed using different models of the well-formation configuration<ref name= "Duffield2007"/><ref name= "Butler1997"/>. In contrast to pumping tests, slug tests provide a ''K'' estimate that is primarily a function of the materials in the vicinity of the screened interval of the test well. Slug test data analyses can be facilitated using software packages like AQTESOLV (Aquifer Test Solver), which has been developed for analyzing different test methods<ref name= "Duffield2007"/>.
  
−
[[File:Allen-King1w2 Fig5.png|thumb|right|400 px|Figure 5. The trichloroethene ''K<sub>oc</sub>'' versus the Hydrogen/Oxygen ratio of carbonaceous material. The sorption coefficient (per gram carbon) is 1-2 orders of magnitude greater for more condensed carbonaceous matter, as indicated by greater H/O ratios, compared to humic acid and peat. Calculations are from linear isotherms at a low aqueous concentration<ref name= "Grathwohl1990"/>.]]
+
Although a slug test is very simple in principle, considerable care must be taken in all stages of a test<ref name= "Butler2005"/><ref name= "Butler1997"/><ref name= "Butler2009"/>. Because test responses are highly sensitive to the materials immediately adjacent to the test well, that well must be appropriately developed before a test is performed. Otherwise, the ''K'' estimate can be biased by a low-''K'' zone (skin) that can form during well construction. In high-''K'' formations, the head recovery is rapid, and pneumatic methods are often used to minimize the time associated with test initiation. In addition, due to the relatively high flow velocity, the impact of pipe hydraulics on pressure readings should be considered when analyzing slug test data from high-''K'' zones<ref name= "Butler2003">Butler Jr, J.J., Garnett, E.J. and Healey, J.M., 2003. Analysis of slug tests in formations of high hydraulic conductivity. Groundwater, 41(5), pp.620-631. [https://doi.org/10.1111/j.1745-6584.2003.tb02400.x doi: 10.1111/j.1745-6584.2003.tb02400.x]</ref>.  In low-''K'' formations, slug tests can take an extremely long time to complete, although test time can be significantly reduced by decreasing the effective casing radius (portion of well in which the water level is changing)<ref name= "Butler1997"/>.
 +
 +
Slug tests can be configured to obtain information about vertical variations in ''K'' along the screened (open) interval of a well. Test intervals can be isolated with straddle packers, and slug tests performed within that isolated interval. The straddle packers can be incrementally moved along the screened interval of a well to characterize the vertical variation of ''K'' at a relatively high resolution. Using a two-packer tool (Fig. 2A), slug tests have been performed in a number of 0.25-m intervals in a well at the Geohydrologic Experimental and Monitoring Site (GEMS) in the Kansas River valley<ref name= "Butler2005"/>.  At each isolated interval, multiple tests are performed, initiated with different head changes, following recommended test guidelines<ref name= "Butler1997"/><ref name= "Butler2009"/>. An example data set is presented in Figure 2B. The multi-level slug test ''K'' estimates compare favorably with estimates obtained using other approaches (Fig. 3).
  
−
==Effect of Carbon Type==
+
<div><ul>
−
Research reviewed by Allen-King et al. (2002)<ref name= "Allenking2002"/> Cornelissen et al. (2004)<ref name= "Cornelissen2004">Cornelissen, G., Kukulska, Z., Kalaitzidis, S., Christanis, K. and Gustafsson, Ö., 2004. Relations between environmental black carbon sorption and geochemical sorbent characteristics. Environmental Science & Technology, 38(13), pp.3632-3640. [http://dx.doi.org/10.1021/es0498742 doi: 10.1021/es0498742]</ref>, and Huang et al. (2003)<ref name= "Huang2003">Huang, W., Peng, P.A., Yu, Z. and Fu, J., 2003. Effects of organic matter heterogeneity on sorption and desorption of organic contaminants by soils and sediments. Applied Geochemistry, 18(7), pp.955-972. [http://dx.doi.org/10.1016/S0883-2927(02)00205-6 doi: 10.1016/S0883-2927(02)00205-6]</ref> indicates that some types of organic matter are much stronger sorbents than others.  Experimental results show that thermally altered carbonaceous materials (TACMs), such as coals, kerogen and black carbons, will sorb greater concentrations of nonpolar organic contaminants than unaltered organic materials per gram of carbon (Fig. 5), especially at low concentrations relative to solubility. TACMs are more condensed than their unaltered precursors, and have a lower oxygen content, and higher aromatic content than unaltered materials.  Sorbed concentrations to TACM can be 10 to 100 times greater at equilibrium than the amount sorbed to less condensed forms of organic matter on a per-g-carbon basis.
+
<li style="display: inline-block;">[[File:Liu1w2 Fig2A.png|thumb|400 px|Figure 2A. Schematic of a falling-head slug test (water flows from well into aquifer) performed in a multi-level slug-test system. Head change is introduced in standpipe, which is directly connected to the interval isolated by the straddle packers (not to scale).]] 
 +
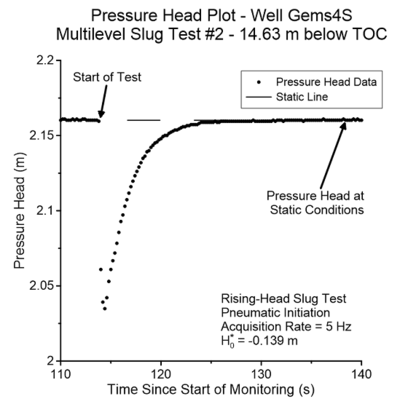
<li style="display: inline-block;">[[File:Liu1w2 Fig2B.png|thumb|400 px|Figure 2B. Example data plot from a multilevel slug test at GEMS. Test is initiated by sudden depressurization of a pressurized air column<ref name= "Butler2003"/>.]]</li>
 +
<li style="display: inline-block;">[[File:Liu1w2 Fig3.png|thumb|400 px|Figure 3. ''K'' estimates from different field methods at GEMS<ref name= "Butler2005"/>. Well DW is located 2 m east of GEMS4S.]]
 +
</ul></div>
  
−
Sorption to TACMs is dominated by adsorptive behavior with strong sorption at low aqueous concentrations, with progressively weaker sorption at higher concentrations<ref name= "Cornelissen2004"/><ref name= "Allenking2002"/><ref name= "Huang2003"/>. This effect is commonly represented with a Freundlich isotherm with the Freundlich exponent <1.  
+
In addition to existing wells, slug tests can also be performed in DP installations so that ''K'' estimates can be obtained virtually at any location in unconsolidated formations. Various approaches have been developed that allow slug tests to be performed at one or multiple levels in a single DP hole<ref>Hinsby, K., Bjerg, P.L., Andersen, L.J., Skov, B. and Clausen, E.V., 1992. A mini slug test method for determination of a local hydraulic conductivity of an unconfined sandy aquifer. Journal of Hydrology, 136(1-4), pp.87-106. [https://doi.org/10.1016/0022-1694(92)90006-H doi: 10.1016/0022-1694(92)90006-H]</ref><ref>Butler Jr, J.J., Healey, J.M., McCall, G.W., Garnett, E.J. and Loheide, S.P., 2002. Hydraulic tests with direct‐push equipment. Groundwater, 40(1), pp.25-36. [https://doi.org/10.1111/j.1745-6584.2002.tb02488.x doi: 10.1111/j.1745-6584.2002.tb02488.x]</ref><ref name= "McCall2002">McCall, W., J.J. Butler, Jr., J.M. Healey, A.A. Lanier, S.M. Sellwood, and E.J. Garnett, 2002. A dual-tube direct-push method for vertical profiling of hydraulic conductivity in unconsolidated formations, Environ. & Eng. Geoscience, 8(2), 75-84.  [https://doi.org/10.2113/gseegeosci.8.2.75 doi: 10.2113/gseegeosci.8.2.75]</ref><ref name= "Sellwood2005">Sellwood, S.M., Healey, J.M., Birk, S. and Butler, J.J., 2005. Direct‐push hydrostratigraphic profiling: coupling electrical logging and slug tests. Ground water, 43(1), pp.19-29. [http://dx.doi.org/10.1111/j.1745-6584.2005.tb02282.x  doi: 10.1111/j.1745-6584.2005.tb02282.x]</ref>.  In McCall et al. (2002)<ref name= "McCall2002"/>, a pair of nested rod strings were driven to the test interval with a solid drive point attached to the end of inner rod string for advancement. Upon reaching the test depth, the drive point and inner rod string were retracted, and a screen was lowered to the bottom of the outer rod string. The outer rod string was pulled up while the screen was held in place, leaving the screen exposed to the surrounding formation. After the slug test was completed in the exposed screen, the screen was removed and the inner rod string with the attached solid drive point was reinserted. The nested rod strings were then driven to the next test depth. In low-''K'' formations such as silts and clays, the formation materials may not collapse completely back to the screen when the outer rod string is pulled up. In this case, the diameter of the borehole can be estimated and used in place of the screen diameter, or the problem can be avoided by using a coring tube of similar size to the screen to create a hole below the end of the outer rod string. Instead of setting the screen by pulling up the outer rod string, the screen can be directly inserted into the hole for slug testing. Regardless of how the screen is set into the formation, it is always recommended that the screen be appropriately developed before slug tests are performed. In low-''K'' formations, development may be limited to scraping the sides of the cored hole with a steel brush and removing the silty water from the screen with a low-flow pump.
  
−
TACMs are typically associated with shale rocks or coal containing kerogen that has been buried and lithified, or with soils containing char or soot from incomplete combustion. This material may be present in consolidated rock or in sediments that contain these materials<ref>Kleineidam, S., Rügner, H., Ligouis, B. and Grathwohl, P., 1999. Organic matter facies and equilibrium sorption of phenanthrene. Environmental Science & Technology, 33(10), pp.1637-1644. [http://dx.doi.org/10.1021/es9806635 doi: 10.1021/es9806635]</ref><ref>Binger, C.A., Martin, J.P., Allen-King, R.M. and Fowler, M., 1999. Variability of chlorinated-solvent sorption associated with oxidative weathering of kerogen. Journal of Contaminant Hydrology, 40(2), pp.137-158. [http://dx.doi.org/10.1016/S0169-7722(99)00047-9 doi: 10.1016/S0169-7722(99)00047-9]</ref>. However, weathering of these materials appears to diminish adsorption<ref name= "Grathwohl1990"> Grathwohl, P., 1990. Influence of organic matter from soils and sediments from various origins on the sorption of some chlorinated aliphatic hydrocarbons: implications on Koc correlations. Environmental Science & Technology, 24(11), pp.1687-1693. [http://dx.doi.org/10.1021/es00081a010 doi: 10.1021/es00081a010]</ref>.
+
Sellwood et al. (2005)<ref name= "Sellwood2005"/> proposed a modification of the approach by McCall et al. (2002)<ref name= "McCall2002"/> to reduce profiling time and gain more information about subsurface stratigraphy. Instead of performing slug tests on the way down, slug tests were performed at different depths as the outer rod string was pulled up (Fig. 4). This way, the number of changes between the outer and inner rod strings was minimized (i.e., only one change needed at the bottom of the profile). Furthermore, an electrical conductivity (EC) probe was attached to the inner rod string so that EC data could be collected as the rod strings were advanced; the EC data could then be used for selecting the intervals for slug tests as the rod strings were retracted. This approach, called hydrostratigraphic profiling, enabled the collection of information on electrical and hydraulic conductivity to be obtained at a speed and resolution that had previously not been possible.
  
−
==How to Estimate Sorption?==
 
−
For high contaminant concentrations or when amorphous organic matter dominates sorption, measurements of soil ''f<sub>oc</sub>'' and empirical correlations with contaminant properties appear to provide ''K<sub>d</sub>'' estimates within about a factor of 3 of values measured in laboratory isotherms<ref name= "Allenking2002"/>.  However, when TACMs are present and contaminant concentrations are low, the empirical correlations may substantially underestimate sorption.  Additional research is needed to determine when simple empirical correlations may be used to estimate ''K<sub>d</sub>'' and when more rigorous experimental investigations are required.
 
  
−
==Summary==
 
−
Nonionic and nonpolar organic contaminants including chlorinated solvents and petroleum hydrocarbons can become associated with solid phase organic matter in the soil, sediment, and rock.  When amorphous organic matter is the primary sorbent, sorption is linear and distribution coefficients can be estimated from empirical correlations with contaminant properties (aqueous solubility or octanol-water partition coefficient) and site-specific measurements of solid phase organic carbon.  However, when thermally altered carbonaceous materials (TACMs) are present, sorption may be non-linear and the empirical correlations may substantially underestimate sorption at low contaminant concentrations.
 
  
 
==References==
 
==References==

Revision as of 20:17, 1 April 2019


Related Article(s):


CONTRIBUTOR(S): Gaisheng Liu and Jim Butler

Key Resource(s):

Introduction

Hydraulic conductivity is mathematically defined as the parameter K in Darcy’s Law[4] (see Fig. 1),

Liu1w2 Eq1.png

where:
Q is the flow rate across area A of a porous medium,
K is the hydraulic conductivity, and
i is the hydraulic gradient, which can be computed as:

Liu1w2 Eq2.png

where:
h1 and h2     are the hydraulic heads at the ends of the experimental domain, and
L is the total length.
Figure 1. Schematic of Darcy’s Law flow experiment.

Hydraulic conductivity is dependent on the properties of both water and the porous medium,

Liu1w2 Eq3.png

where:
k is the intrinsic permeability of the medium, a parameter which is solely dependent on the geometry of the interconnected pores,
g is the gravitational constant,
ρ is the density of the pore water, and
μ is the dynamic viscosity of the pore water, respectively.

Many approaches have been developed to characterize K[1]. These approaches can be grouped into two general categories based on how the K estimates are obtained:

  • hydraulic methods that involve water injection or extraction and the measurement of the induced pressure response, and
  • indirect methods that rely on empirical correlations, often site-specific in nature, between K and other more readily evaluated formation properties (e.g., resistance to electric current).

Because hydraulic methods can be directly related to the mathematical definition of K through Darcy’s Law, K estimates obtained with those methods are generally considered to be more reliable than those obtained with indirect methods.

Other classifications of K characterization approaches are possible. For example, approaches can be divided into those based on data collected in the field and those based on measurements on core samples in the laboratory. In the latter case, there can be considerable uncertainty about how representative the core sample is of field conditions.

Field-based approaches can be further subdivided based on whether the measurement is conducted in the subsurface or on the surface. Subsurface measurements provide the most reliable information about K variations at the scale needed for environmental site investigations. Nearly all field-based hydraulic methods are performed in the subsurface and require either boreholes or direct push (DP) installations for extracting or injecting water and monitoring the induced head changes. Compared to methods that rely on existing wells, DP approaches can be applied essentially wherever K information is needed, thus greatly expanding the spatial coverage of K measurement in the field. DP approaches, however, are generally limited to use in relatively shallow (20-30 m from land surface) unconsolidated settings.

Field K measurements can also be performed on the land surface or in an aircraft. Most of these are geophysical approaches that involve measuring electrical, magnetic, or seismic properties of the formation and then transforming them into K estimates using empirical relations. The biggest advantage of surface or airborne approaches is their minimal site disturbance, as no subsurface boring is needed. However, the resolution that can be provided is limited, as the measurements are typically affected by conditions over a relatively large volume of the formation. Geophysical methods can also be performed in boreholes. Borehole geophysical methods can provide a much higher resolution description of K than surface-based methods.

The scale of measurement is an important factor to consider when assessing various approaches. For water-supply investigations, a single estimate of K averaged over a large volume of an aquifer will usually suffice; such an estimate is commonly obtained via pumping tests in a well[3]. For water-quality investigations, however, K estimates over a large measurement volume are often of limited value[5]. In that case, small-scale K measurements that provide information about local geological controls on groundwater flow and transport are usually required to obtain reliable predictions of contaminant behavior and to design effective remediation systems.

In this article, we focus on the approaches that can be used to obtain small-scale, localized measurements of K for environmental site investigations. Only the more commonly used approaches are discussed. Some other approaches, such as dipole flow tests[6][7], tracer tests[8], or hydraulic tomography[9][10] will not be discussed here.

Hydraulic Testing Approaches

Pumping Tests

The pumping test is the most common method for determining K over a relatively large volume of an aquifer in water-supply investigations[5]. During a typical test, the pumping rate is kept constant, although it can be varied in time to obtain better signal-to-noise ratios in the acquired data[11]. In the constant-rate approach, a well, preferably centrally located at the site, is pumped while induced head changes are monitored at that and nearby wells. The head changes, along with the pumping rate, can then be used to estimate aquifer parameters using different models of the well-aquifer configuration[12][13]. Pumping test analyses can be facilitated using software packages like AQTESOLV (Aquifer Test Solver), which has been developed for analyzing different types of aquifer tests[14].

Pumping tests are primarily performed to obtain large-scale volumetric averages of aquifer parameters as well as information about aquifer boundaries. However, one form of the pumping test, the step-drawdown test, is specifically directed at getting information about the efficiency of the pumping well. The K estimate from a pumping test is an average over a large volume of the formation and does not provide information at the scale of most relevance for issues involving contaminant transport (e.g., meters or less). Thus, pumping tests are less commonly employed for environmental site investigations[5].

Slug Tests

The slug test is one of the most common methods for determining K at the scale of relevance for environmental site investigations[15][5]. Slug tests are typically performed in existing wells at multiple horizontal and vertical locations across the site to characterize the spatial distribution of K values. However, slug tests can also be performed in temporary installations such as DP rods. In this approach, a near-instantaneous head change is applied in the well or DP rods and the subsequent head recovery is used to estimate K. The initial head change can be introduced using a solid object (slug), compressed gas (pneumatic system), or by the addition/removal of a certain amount of water[15]. The recovery data can be analyzed using different models of the well-formation configuration[14][15]. In contrast to pumping tests, slug tests provide a K estimate that is primarily a function of the materials in the vicinity of the screened interval of the test well. Slug test data analyses can be facilitated using software packages like AQTESOLV (Aquifer Test Solver), which has been developed for analyzing different test methods[14].

Although a slug test is very simple in principle, considerable care must be taken in all stages of a test[1][15][5]. Because test responses are highly sensitive to the materials immediately adjacent to the test well, that well must be appropriately developed before a test is performed. Otherwise, the K estimate can be biased by a low-K zone (skin) that can form during well construction. In high-K formations, the head recovery is rapid, and pneumatic methods are often used to minimize the time associated with test initiation. In addition, due to the relatively high flow velocity, the impact of pipe hydraulics on pressure readings should be considered when analyzing slug test data from high-K zones[16]. In low-K formations, slug tests can take an extremely long time to complete, although test time can be significantly reduced by decreasing the effective casing radius (portion of well in which the water level is changing)[15].

Slug tests can be configured to obtain information about vertical variations in K along the screened (open) interval of a well. Test intervals can be isolated with straddle packers, and slug tests performed within that isolated interval. The straddle packers can be incrementally moved along the screened interval of a well to characterize the vertical variation of K at a relatively high resolution. Using a two-packer tool (Fig. 2A), slug tests have been performed in a number of 0.25-m intervals in a well at the Geohydrologic Experimental and Monitoring Site (GEMS) in the Kansas River valley[1]. At each isolated interval, multiple tests are performed, initiated with different head changes, following recommended test guidelines[15][5]. An example data set is presented in Figure 2B. The multi-level slug test K estimates compare favorably with estimates obtained using other approaches (Fig. 3).

  • Figure 2A. Schematic of a falling-head slug test (water flows from well into aquifer) performed in a multi-level slug-test system. Head change is introduced in standpipe, which is directly connected to the interval isolated by the straddle packers (not to scale).
  • Figure 2B. Example data plot from a multilevel slug test at GEMS. Test is initiated by sudden depressurization of a pressurized air column[16].
  • Figure 3. K estimates from different field methods at GEMS[1]. Well DW is located 2 m east of GEMS4S.

In addition to existing wells, slug tests can also be performed in DP installations so that K estimates can be obtained virtually at any location in unconsolidated formations. Various approaches have been developed that allow slug tests to be performed at one or multiple levels in a single DP hole[17][18][19][20]. In McCall et al. (2002)[19], a pair of nested rod strings were driven to the test interval with a solid drive point attached to the end of inner rod string for advancement. Upon reaching the test depth, the drive point and inner rod string were retracted, and a screen was lowered to the bottom of the outer rod string. The outer rod string was pulled up while the screen was held in place, leaving the screen exposed to the surrounding formation. After the slug test was completed in the exposed screen, the screen was removed and the inner rod string with the attached solid drive point was reinserted. The nested rod strings were then driven to the next test depth. In low-K formations such as silts and clays, the formation materials may not collapse completely back to the screen when the outer rod string is pulled up. In this case, the diameter of the borehole can be estimated and used in place of the screen diameter, or the problem can be avoided by using a coring tube of similar size to the screen to create a hole below the end of the outer rod string. Instead of setting the screen by pulling up the outer rod string, the screen can be directly inserted into the hole for slug testing. Regardless of how the screen is set into the formation, it is always recommended that the screen be appropriately developed before slug tests are performed. In low-K formations, development may be limited to scraping the sides of the cored hole with a steel brush and removing the silty water from the screen with a low-flow pump.

Sellwood et al. (2005)[20] proposed a modification of the approach by McCall et al. (2002)[19] to reduce profiling time and gain more information about subsurface stratigraphy. Instead of performing slug tests on the way down, slug tests were performed at different depths as the outer rod string was pulled up (Fig. 4). This way, the number of changes between the outer and inner rod strings was minimized (i.e., only one change needed at the bottom of the profile). Furthermore, an electrical conductivity (EC) probe was attached to the inner rod string so that EC data could be collected as the rod strings were advanced; the EC data could then be used for selecting the intervals for slug tests as the rod strings were retracted. This approach, called hydrostratigraphic profiling, enabled the collection of information on electrical and hydraulic conductivity to be obtained at a speed and resolution that had previously not been possible.


References

  1. ^ 1.0 1.1 1.2 1.3 1.4 Butler, J.J., 2005. Hydrogeological methods for estimation of spatial variations in hydraulic conductivity. In Hydrogeophysics (pp. 23-58). Springer, Dordrecht. doi: 10.1007/1-4020-3102-5_2
  2. ^ Liu, G., Butler, J.J., Reboulet, E. and Knobbe, S., 2012. Hydraulic conductivity profiling with direct push methods. Grundwasser, 17(1), pp.19-29. doi: 10.1007/s00767-011-0182-9
  3. ^ 3.0 3.1 Freeze, R.A., Cherry, J.A. and Groundwater., A., 1979. Prentice-Hall. Inc., Englewood Cliffs, NJ ISBN 0-13-365312-9.
  4. ^ Darcy, H. (1856). Les Fontaines Publiques de la Ville de Dijon, Dalmont, Paris. doi: 10.1029/2001WR000727
  5. ^ 5.0 5.1 5.2 5.3 5.4 5.5 Butler Jr, J.J., 2009. Pumping tests for aquifer evaluation - Time for a change?. Groundwater, 47(5), pp.615-617. doi: 10.1111/j.1745-6584.2008.00488.x
  6. ^ Kabala, Z.J., 1993. The dipole flow test: A new single‐borehole test for aquifer characterization. Water Resources Research, 29(1), pp.99-107. doi: 10.1029/92WR01820
  7. ^ Zlotnik, V.A. and Zurbuchen, B.R., 1998. Dipole probe: Design and field applications of a single‐borehole device for measurements of vertical variations of hydraulic conductivity. Groundwater, 36(6), pp.884-893. doi: 10.1111/j.1745-6584.1998.tb02095.x
  8. ^ Datta‐Gupta, A., Yoon, S., Vasco, D.W. and Pope, G.A., 2002. Inverse modeling of partitioning interwell tracer tests: A streamline approach. Water Resources Research, 38(6), pp.15-1. doi: 10.1029/2001WR000597
  9. ^ Yeh, T.C.J. and Liu, S., 2000. Hydraulic tomography: Development of a new aquifer test method. Water Resources Research, 36(8), pp.2095-2105. Report.pdf
  10. ^ Bohling, G.C. and Butler Jr, J.J., 2010. Inherent limitations of hydraulic tomography. Groundwater, 48(6), pp.809-824. doi: 10.1111/j.1745-6584.2010.00757.x
  11. ^ Rasmussen, T.C., Haborak, K.G. and Young, M.H., 2003. Estimating aquifer hydraulic properties using sinusoidal pumping at the Savannah River site, South Carolina, USA. Hydrogeology Journal, 11(4), pp.466-482. doi: 10.1007/s10040-003-0255-7
  12. ^ Batu, V., 1998. Aquifer hydraulics: a comprehensive guide to hydrogeologic data analysis. John Wiley & Sons.
  13. ^ Kruseman, G.P., De Ridder, N.A. and Verweij, J.M., 1990. Analysis and evaluation of pumping test data – ILRI Pub. 47. The Netherlands: International institute for land reclamation and improvement
  14. ^ 14.0 14.1 14.2 Duffield, G.M., 2007. AQTESOLV for Windows Version 4.5 User's Guide. HydroSOLVE, Reston, VA.
  15. ^ 15.0 15.1 15.2 15.3 15.4 15.5 Butler Jr, J.J., 1997. The design, performance, and analysis of slug tests. Crc Press.
  16. ^ 16.0 16.1 Butler Jr, J.J., Garnett, E.J. and Healey, J.M., 2003. Analysis of slug tests in formations of high hydraulic conductivity. Groundwater, 41(5), pp.620-631. doi: 10.1111/j.1745-6584.2003.tb02400.x
  17. ^ Hinsby, K., Bjerg, P.L., Andersen, L.J., Skov, B. and Clausen, E.V., 1992. A mini slug test method for determination of a local hydraulic conductivity of an unconfined sandy aquifer. Journal of Hydrology, 136(1-4), pp.87-106. doi: 10.1016/0022-1694(92)90006-H
  18. ^ Butler Jr, J.J., Healey, J.M., McCall, G.W., Garnett, E.J. and Loheide, S.P., 2002. Hydraulic tests with direct‐push equipment. Groundwater, 40(1), pp.25-36. doi: 10.1111/j.1745-6584.2002.tb02488.x
  19. ^ 19.0 19.1 19.2 McCall, W., J.J. Butler, Jr., J.M. Healey, A.A. Lanier, S.M. Sellwood, and E.J. Garnett, 2002. A dual-tube direct-push method for vertical profiling of hydraulic conductivity in unconsolidated formations, Environ. & Eng. Geoscience, 8(2), 75-84. doi: 10.2113/gseegeosci.8.2.75
  20. ^ 20.0 20.1 Sellwood, S.M., Healey, J.M., Birk, S. and Butler, J.J., 2005. Direct‐push hydrostratigraphic profiling: coupling electrical logging and slug tests. Ground water, 43(1), pp.19-29. doi: 10.1111/j.1745-6584.2005.tb02282.x

See Also

Retrieved from "https://www.enviro.wiki/index.php?title=User:Debra_Tabron/sandbox&oldid=12456"