Difference between revisions of "Long-Term Monitoring (LTM) - Data Analysis"
m (1 revision imported) |
(Tag: Visual edit) |
||
| (18 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
<div style="float:right;margin:0 0 2em 2em;">__TOC__</div> | <div style="float:right;margin:0 0 2em 2em;">__TOC__</div> | ||
'''Related Article(s):''' | '''Related Article(s):''' | ||
| + | |||
*[[Long-Term Monitoring (LTM)]] | *[[Long-Term Monitoring (LTM)]] | ||
*[[Long-Term Monitoring (LTM) - Data Variability]] | *[[Long-Term Monitoring (LTM) - Data Variability]] | ||
| − | ''' | + | '''Contributor(s):''' [[Dr. Thomas McHugh]] and [[Dr. David Adamson, P.E.]] |
'''Key Resource(s):''' | '''Key Resource(s):''' | ||
| − | *[ | + | |
| + | *[//www.enviro.wiki/images/9/9e/ITRC-2013-Groundwater_Stat_Mon.pdf Groundwater statistics and monitoring compliance, statistical tools for the project life cycle]<ref name="ITCR2013">ITRC, 2013. Groundwater statistics and monitoring compliance, statistical tools for the project life cycle. GSMC-1. Washington, D.C.: Interstate Technology & Regulatory Council, Groundwater Statistics and Monitoring Compliance Team. [//www.enviro.wiki/images/9/9e/ITRC-2013-Groundwater_Stat_Mon.pdf Report pdf]</ref> | ||
*[https://www.serdp-estcp.org/Program-Areas/Environmental-Restoration/Contaminated-Groundwater/Monitoring/ER-201209 Methods for minimization and management of variability in long-term groundwater monitoring results-ER-201209]<ref name="McHugh2015">McHugh, T.E., Kulkarni, P.R., Beckley, L.M., Newell, C.J., Strasters, B., 2015. Methods for minimization and management of variability in long-term groundwater monitoring results. A new method to optimize monitoring frequency and evaluate long-term concentration trends, Technical Report, Task 2 & 3. ER-201209. [https://www.serdp-estcp.org/Program-Areas/Environmental-Restoration/Contaminated-Groundwater/Monitoring/ER-201209 ER-201209]</ref> | *[https://www.serdp-estcp.org/Program-Areas/Environmental-Restoration/Contaminated-Groundwater/Monitoring/ER-201209 Methods for minimization and management of variability in long-term groundwater monitoring results-ER-201209]<ref name="McHugh2015">McHugh, T.E., Kulkarni, P.R., Beckley, L.M., Newell, C.J., Strasters, B., 2015. Methods for minimization and management of variability in long-term groundwater monitoring results. A new method to optimize monitoring frequency and evaluate long-term concentration trends, Technical Report, Task 2 & 3. ER-201209. [https://www.serdp-estcp.org/Program-Areas/Environmental-Restoration/Contaminated-Groundwater/Monitoring/ER-201209 ER-201209]</ref> | ||
| Line 25: | Line 27: | ||
Site managers often use parametric or non-parametric statistica methods to analyze LTM groundwater concentration vs. time data. [[wikipedia: Parametric statistics | Parametric statistical methods]] incorporate specific assumptions regarding the data distribution (e.g., a normal distribution or a log normal distribution), while [[wikipedia: Nonparametric statistics | non-parametric methods]] do not. Parametric methods are more accurate and powerful for the analysis of datasets that satisfy the specified assumptions. However, non-parametric methods are more accurate for datasets that do not satisfy the required assumptions that are incorporated into the specific parametric methods. Site managers commonly choose between one parametric method (linear regression) and two non-parametric methods (Mann-Kendall and Theil-Sen Slope Estimator<ref>Gilbert, R.O., 1987. Statistical methods for environmental pollution monitoring. John Wiley & Sons. ISBN 978-0-471-28878-7</ref>) to evaluate concentration trends over time. Mann-Kendall can only be used to evaluate the concentration trend (i.e., are concentrations increasing or decreasing?) with linear regression and the Theil-Sen Slope Estimator can be used to evaluate both concentration trends and attenuation rates. When evaluating concentration vs. time with groundwater monitoring data, the long-term concentration trend is most commonly assumed to be first-order (e.g., exponential decay). This first-order attenuation rate is estimated using linear regression or the Theil-Sen Slope Estimator on natural log transformed concentration data (i.e., Ln(C)) vs. time. The site manager may conduct trend analysis for individual monitoring wells or for the plume as a whole (i.e., using a representation of plume mass or average plume concentration). | Site managers often use parametric or non-parametric statistica methods to analyze LTM groundwater concentration vs. time data. [[wikipedia: Parametric statistics | Parametric statistical methods]] incorporate specific assumptions regarding the data distribution (e.g., a normal distribution or a log normal distribution), while [[wikipedia: Nonparametric statistics | non-parametric methods]] do not. Parametric methods are more accurate and powerful for the analysis of datasets that satisfy the specified assumptions. However, non-parametric methods are more accurate for datasets that do not satisfy the required assumptions that are incorporated into the specific parametric methods. Site managers commonly choose between one parametric method (linear regression) and two non-parametric methods (Mann-Kendall and Theil-Sen Slope Estimator<ref>Gilbert, R.O., 1987. Statistical methods for environmental pollution monitoring. John Wiley & Sons. ISBN 978-0-471-28878-7</ref>) to evaluate concentration trends over time. Mann-Kendall can only be used to evaluate the concentration trend (i.e., are concentrations increasing or decreasing?) with linear regression and the Theil-Sen Slope Estimator can be used to evaluate both concentration trends and attenuation rates. When evaluating concentration vs. time with groundwater monitoring data, the long-term concentration trend is most commonly assumed to be first-order (e.g., exponential decay). This first-order attenuation rate is estimated using linear regression or the Theil-Sen Slope Estimator on natural log transformed concentration data (i.e., Ln(C)) vs. time. The site manager may conduct trend analysis for individual monitoring wells or for the plume as a whole (i.e., using a representation of plume mass or average plume concentration). | ||
| − | Most statistics software packages can be used for parametric or non-parametric trend analysis. In addition, organizations have developed a number of free software programs specifically for analysis of environmental monitoring data (see Appendix D of ITRC, 2013)<ref name="ITCR2013"/>. Commonly used software tools include: | + | Most statistics software packages can be used for parametric or non-parametric trend analysis. In addition, organizations have developed a number of free software programs specifically for analysis of environmental monitoring data (see Appendix D of ITRC, 2013)<ref name="ITCR2013" />. Commonly used software tools include: |
*<u>Microsoft Excel</u>: Parametric trend analyses can be conducted using Excel functions or the Data Analysis Tool Pack add-in that is part of the Excel software package, but may not be installed on your computer if the default installation option was chosen. | *<u>Microsoft Excel</u>: Parametric trend analyses can be conducted using Excel functions or the Data Analysis Tool Pack add-in that is part of the Excel software package, but may not be installed on your computer if the default installation option was chosen. | ||
| − | *<u>[https://www.epa.gov/land-research/proucl-software ProUCL (Free)]</u>: Supports parametric and non-parametric analyses<ref> Singh, A., Maichle, R. and Lee, S.E., 2006. On the computation of a 95% upper confidence limit of the unknown population mean based upon data sets with below detection limit observations. U.S. Environmental Protection Agency, EPA-600-R-06-022. [ | + | *<u>[https://www.epa.gov/land-research/proucl-software ProUCL (Free)]</u>: Supports parametric and non-parametric analyses<ref> Singh, A., Maichle, R. and Lee, S.E., 2006. On the computation of a 95% upper confidence limit of the unknown population mean based upon data sets with below detection limit observations. U.S. Environmental Protection Agency, EPA-600-R-06-022. [//www.enviro.wiki/images/4/4c/Singh_EPA-2006-Computation.pdf Report pdf]</ref>. |
| − | *<u>[http://www.gsi-net.com/en/software/free-software/monitoring-and-remediation-optimization-system-maros-version-2-2.html MAROS (Free)]</u>: Supports spatial data averaging for whole plume trend analysis<ref >AFCEC (Air Force Civil Engineer Center), 2012. Monitoring and remediation optimization system (MAROS) software, user's guide and technical manual. In: Air Force Center for Environmental Excellence. [http://www.gsi-net.com/en/software/free-software/monitoring-and-remediation-optimization-system-maros-version-2-2.html MAROS]</ref>. | + | *<u>[[http://www.gsi-net.com/en/software/free-software/monitoring-and-remediation-optimization-system-maros-version-2-2.html MAROS (Free)]</u>: Supports spatial data averaging for whole plume trend analysis<ref>AFCEC (Air Force Civil Engineer Center), 2012. Monitoring and remediation optimization system (MAROS) software, user's guide and technical manual. In: Air Force Center for Environmental Excellence. [http://www.gsi-net.com/en/software/free-software/monitoring-and-remediation-optimization-system-maros-version-2-2.html MAROS]</ref>. |
*<u>[http://www.gsi-net.com/en/software/free-software/gsi-mann-kendall-toolkit.html Mann-Kendall Tool Kit (Free)]</u>: Evaluates concentration trends using the Mann-Kendall statistical test<ref>Connor, J.A., Farhat, S.K. and Vanderford, M., 2014. GSI Mann‐Kendall toolkit for quantitative analysis of plume concentration trends. Groundwater, 52(6), 819-820. [http://dx.doi.org/10.1111/gwat.12277 doi: 10.1111/gwat.12277]</ref>. | *<u>[http://www.gsi-net.com/en/software/free-software/gsi-mann-kendall-toolkit.html Mann-Kendall Tool Kit (Free)]</u>: Evaluates concentration trends using the Mann-Kendall statistical test<ref>Connor, J.A., Farhat, S.K. and Vanderford, M., 2014. GSI Mann‐Kendall toolkit for quantitative analysis of plume concentration trends. Groundwater, 52(6), 819-820. [http://dx.doi.org/10.1111/gwat.12277 doi: 10.1111/gwat.12277]</ref>. | ||
==How Much Data is Needed?== | ==How Much Data is Needed?== | ||
| − | For statistical analyses, more data (e.g., more groundwater monitoring events over a longer time period) yields a more accurate analysis (i.e., a smaller [[wikipedia: p-value | p-value]] or a smaller [[wikipedia: Confidence interval | confidence interval | + | For statistical analyses, more data (e.g., more groundwater monitoring events over a longer time period) yields a more accurate analysis (i.e., a smaller [[wikipedia: p-value | p-value]] or a smaller [[wikipedia: Confidence interval | confidence interval]). The amount of monitoring data needed to characterize the long-term attenuation rate with a defined level of accuracy (i.e., a confidence interval less than a defined threshold) or confidence (i.e., a p-value less than a defined level) depends on the site-specific long-term attenuation rate and the magnitude of short-term variability. Less data are required for a site with fast attenuation and low short-term variability. More data are required for a site with slow attenuation and high short-term variability. |
| − | |||
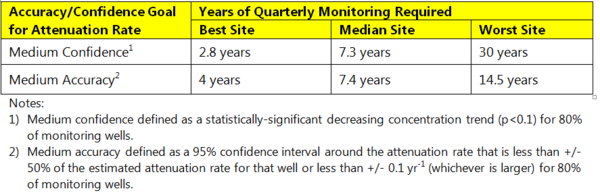
[[File:Adamson-Article 2-Table 1.PNG|thumbnail|right|600 px|Table 1. Monitoring data required to determine long-term attenuation rate.]] | [[File:Adamson-Article 2-Table 1.PNG|thumbnail|right|600 px|Table 1. Monitoring data required to determine long-term attenuation rate.]] | ||
| − | Researchers analyzed historical monitoring records from 20 sites in order to characterize the range of monitoring data requirements at different sites as part of an ESTCP-funded project<ref name="McHugh2015"/>. At each site, they used historical monitoring data to determine attenuation rate and the site-specific magnitude of short-term variability. Next, they used these values to determine how much monitoring data were required to characterize the long-term attenuation rate within a defined level of accuracy or confidence (Table 1). | + | Researchers analyzed historical monitoring records from 20 sites in order to characterize the range of monitoring data requirements at different sites as part of an ESTCP-funded project<ref name="McHugh2015" />. At each site, they used historical monitoring data to determine attenuation rate and the site-specific magnitude of short-term variability. Next, they used these values to determine how much monitoring data were required to characterize the long-term attenuation rate within a defined level of accuracy or confidence (Table 1). |
This evaluation showed that '''''characterization of long-term trends with either medium confidence or medium accuracy almost always requires four or more years of quarterly monitoring data'''''. The researchers defined medium confidence as a p-value = 0.1, lower than the typical threshold for statistical confidence of 0.05. Longer monitoring times would be required to obtain p-values of 0.05 in most monitoring wells. Additional key findings were: | This evaluation showed that '''''characterization of long-term trends with either medium confidence or medium accuracy almost always requires four or more years of quarterly monitoring data'''''. The researchers defined medium confidence as a p-value = 0.1, lower than the typical threshold for statistical confidence of 0.05. Longer monitoring times would be required to obtain p-values of 0.05 in most monitoring wells. Additional key findings were: | ||
| + | |||
*It is important to recognize that apparent trends characterized using too little data can be misleading and may result in inappropriate management decisions. | *It is important to recognize that apparent trends characterized using too little data can be misleading and may result in inappropriate management decisions. | ||
*When evaluating [[Monitored Natural Attenuation (MNA) | natural attenuation]], there are often situations where the project manager can be confident that contaminant concentrations are decreasing, but highly uncertain as to when numerical clean-up goals will be attained. | *When evaluating [[Monitored Natural Attenuation (MNA) | natural attenuation]], there are often situations where the project manager can be confident that contaminant concentrations are decreasing, but highly uncertain as to when numerical clean-up goals will be attained. | ||
| Line 47: | Line 49: | ||
==Trade-off Between Monitoring Frequency and Duration== | ==Trade-off Between Monitoring Frequency and Duration== | ||
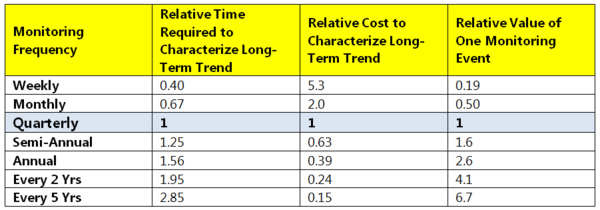
Although the absolute time (or number) of monitoring events required to characterize long-term attenuation rate depends on the short-term variability and the attenuation rate, the trade-off between monitoring frequency and time is independent of these parameters. If you reduce monitoring frequency (e.g., from quarterly to semi-annual monitoring), then you need to extend the total monitoring time in order to characterize the long-term attenuation rate with the same level of confidence or accuracy. The trade-off between monitoring frequency and time required to characterize the long-term trend is defined by the mathematics of linear regression and is the same at every site<ref name="McHugh2016">McHugh , T.E., Kulkarni, P.R., and Newell, C.J., 2016. Time Vs. Money: A Quantitative Evaluation of Monitoring Frequency Vs. Monitoring Duration. Groundwater, 54, 692–698. [http://dx.doi.org/10.1111/gwat.12407 doi: 10.1111/gwat.12407]</ref>. At all sites, five years of semi-annual monitoring data (10 monitoring events total) provides the same information about the long-term attenuation as four years of quarterly monitoring data (16 monitoring events) regardless of the inherent level of event-to-event variability at the site. Thus, switching from quarterly to semi-annual monitoring will reduce the number of monitoring events needed to characterize the long-term trend by 38%, but the amount of time needed will increase by 25%. The trade-off between monitoring frequency and monitoring duration is summarized in Table 2. | Although the absolute time (or number) of monitoring events required to characterize long-term attenuation rate depends on the short-term variability and the attenuation rate, the trade-off between monitoring frequency and time is independent of these parameters. If you reduce monitoring frequency (e.g., from quarterly to semi-annual monitoring), then you need to extend the total monitoring time in order to characterize the long-term attenuation rate with the same level of confidence or accuracy. The trade-off between monitoring frequency and time required to characterize the long-term trend is defined by the mathematics of linear regression and is the same at every site<ref name="McHugh2016">McHugh , T.E., Kulkarni, P.R., and Newell, C.J., 2016. Time Vs. Money: A Quantitative Evaluation of Monitoring Frequency Vs. Monitoring Duration. Groundwater, 54, 692–698. [http://dx.doi.org/10.1111/gwat.12407 doi: 10.1111/gwat.12407]</ref>. At all sites, five years of semi-annual monitoring data (10 monitoring events total) provides the same information about the long-term attenuation as four years of quarterly monitoring data (16 monitoring events) regardless of the inherent level of event-to-event variability at the site. Thus, switching from quarterly to semi-annual monitoring will reduce the number of monitoring events needed to characterize the long-term trend by 38%, but the amount of time needed will increase by 25%. The trade-off between monitoring frequency and monitoring duration is summarized in Table 2. | ||
| − | [[File:Adamson-Article 2-Table 2-Trade-off.PNG|thumbnail|center|600 px|Table 2. Trade-off between monitoring frequency and time. Note: Relative cost is the same as the relative total number of monitoring events required (i.e., based on the assumption that cost is proportional to number of monitoring events) (see McHugh et al., 2006<ref name="McHugh2016"/> for derivation of these relationships).]] | + | [[File:Adamson-Article 2-Table 2-Trade-off.PNG|thumbnail|center|600 px|Table 2. Trade-off between monitoring frequency and time. Note: Relative cost is the same as the relative total number of monitoring events required (i.e., based on the assumption that cost is proportional to number of monitoring events) (see McHugh et al., 2006<ref name="McHugh2016" /> for derivation of these relationships).]] |
==Summary== | ==Summary== | ||
| Line 54: | Line 56: | ||
==References== | ==References== | ||
| − | <references/> | + | <references /> |
==See Also== | ==See Also== | ||
| + | |||
*[http://www.graphpad.com/quickcalcs/linear1/ Linear Regression Calculator]<br /> | *[http://www.graphpad.com/quickcalcs/linear1/ Linear Regression Calculator]<br /> | ||
*[http://www.singlecaseresearch.org/calculators/theil-sen The Thiel-Sen Calculator]<br /> | *[http://www.singlecaseresearch.org/calculators/theil-sen The Thiel-Sen Calculator]<br /> | ||
*[http://www.danielsoper.com/statcalc/calculator.aspx?id=1 A-Priori Sample Size For Multiple Regression Calculator] | *[http://www.danielsoper.com/statcalc/calculator.aspx?id=1 A-Priori Sample Size For Multiple Regression Calculator] | ||
| − | *[https://www.serdp-estcp.org/Program-Areas/Environmental-Restoration/Contaminated-Groundwater/Monitoring/ER-200629 | + | *[https://www.serdp-estcp.org/Program-Areas/Environmental-Restoration/Contaminated-Groundwater/Monitoring/ER-200629 Adaptive Long-Term Monitoring at Environmental Restoration Sites] |
| − | *[https://www.serdp-estcp.org/Program-Areas/Environmental-Restoration/Contaminated-Groundwater/Monitoring/ER-200714 | + | *[https://www.serdp-estcp.org/Program-Areas/Environmental-Restoration/Contaminated-Groundwater/Monitoring/ER-200714 Demonstration and Validation of GTS Long-Term Monitoring Optimization Software at Military and Government Sites] |
Latest revision as of 17:01, 26 April 2022
Site managers commonly use long-term monitoring data to assess changes in contaminant concentrations over time. Statistical methods available in a variety of software packages are used to distinguish between real long-term changes in concentration and apparent changes associated with random variation and short-term fluctuations. When quarterly monitoring is conducted, studies suggest that long-term monitoring activities must be conducted for at least 4 years to obtain a moderately accurate evaluation of the long-term concentration change. With less frequent monitoring (i.e., semi-annual or annual), a somewhat longer monitoring period is required. However, this may be balanced by a reduction in the overall cost of the monitoring program.
Related Article(s):
Contributor(s): Dr. Thomas McHugh and Dr. David Adamson, P.E.
Key Resource(s):
- Groundwater statistics and monitoring compliance, statistical tools for the project life cycle[1]
- Methods for minimization and management of variability in long-term groundwater monitoring results-ER-201209[2]
Introduction
For sites where the initial investigation has been completed and the remedy has been implemented or is under development, the primary objective of continued groundwater monitoring is to track long-term changes in contaminant concentrations. Site managers use these long-term changes to evaluate the effectiveness of site remedies (e.g., natural attenuation or long-duration active remediation such as pump and treat). Other long-term monitoring (LTM) objectives may include protection of a receptor or sentinel well or verification of hydraulic control.
To evaluate remediation progress, a site manager will typically conduct a trend analysis of contaminant concentration vs. time from the monitoring results. A site manager can use the trend analysis to answer two key questions related to groundwater monitoring:
- Are contaminant concentrations decreasing over time?
- What is the attenuation rate and when will the site remediation goals be attained?
Analysis Methods
Site managers often use parametric or non-parametric statistica methods to analyze LTM groundwater concentration vs. time data. Parametric statistical methods incorporate specific assumptions regarding the data distribution (e.g., a normal distribution or a log normal distribution), while non-parametric methods do not. Parametric methods are more accurate and powerful for the analysis of datasets that satisfy the specified assumptions. However, non-parametric methods are more accurate for datasets that do not satisfy the required assumptions that are incorporated into the specific parametric methods. Site managers commonly choose between one parametric method (linear regression) and two non-parametric methods (Mann-Kendall and Theil-Sen Slope Estimator[3]) to evaluate concentration trends over time. Mann-Kendall can only be used to evaluate the concentration trend (i.e., are concentrations increasing or decreasing?) with linear regression and the Theil-Sen Slope Estimator can be used to evaluate both concentration trends and attenuation rates. When evaluating concentration vs. time with groundwater monitoring data, the long-term concentration trend is most commonly assumed to be first-order (e.g., exponential decay). This first-order attenuation rate is estimated using linear regression or the Theil-Sen Slope Estimator on natural log transformed concentration data (i.e., Ln(C)) vs. time. The site manager may conduct trend analysis for individual monitoring wells or for the plume as a whole (i.e., using a representation of plume mass or average plume concentration).
Most statistics software packages can be used for parametric or non-parametric trend analysis. In addition, organizations have developed a number of free software programs specifically for analysis of environmental monitoring data (see Appendix D of ITRC, 2013)[1]. Commonly used software tools include:
- Microsoft Excel: Parametric trend analyses can be conducted using Excel functions or the Data Analysis Tool Pack add-in that is part of the Excel software package, but may not be installed on your computer if the default installation option was chosen.
- ProUCL (Free): Supports parametric and non-parametric analyses[4].
- [MAROS (Free): Supports spatial data averaging for whole plume trend analysis[5].
- Mann-Kendall Tool Kit (Free): Evaluates concentration trends using the Mann-Kendall statistical test[6].
How Much Data is Needed?
For statistical analyses, more data (e.g., more groundwater monitoring events over a longer time period) yields a more accurate analysis (i.e., a smaller p-value or a smaller [[wikipedia: Confidence interval | confidence interval]). The amount of monitoring data needed to characterize the long-term attenuation rate with a defined level of accuracy (i.e., a confidence interval less than a defined threshold) or confidence (i.e., a p-value less than a defined level) depends on the site-specific long-term attenuation rate and the magnitude of short-term variability. Less data are required for a site with fast attenuation and low short-term variability. More data are required for a site with slow attenuation and high short-term variability.
Researchers analyzed historical monitoring records from 20 sites in order to characterize the range of monitoring data requirements at different sites as part of an ESTCP-funded project[2]. At each site, they used historical monitoring data to determine attenuation rate and the site-specific magnitude of short-term variability. Next, they used these values to determine how much monitoring data were required to characterize the long-term attenuation rate within a defined level of accuracy or confidence (Table 1).
This evaluation showed that characterization of long-term trends with either medium confidence or medium accuracy almost always requires four or more years of quarterly monitoring data. The researchers defined medium confidence as a p-value = 0.1, lower than the typical threshold for statistical confidence of 0.05. Longer monitoring times would be required to obtain p-values of 0.05 in most monitoring wells. Additional key findings were:
- It is important to recognize that apparent trends characterized using too little data can be misleading and may result in inappropriate management decisions.
- When evaluating natural attenuation, there are often situations where the project manager can be confident that contaminant concentrations are decreasing, but highly uncertain as to when numerical clean-up goals will be attained.
- For sites with slow attenuation rates, it may be difficult to prove with statistical confidence that contaminant concentrations are decreasing.
Trade-off Between Monitoring Frequency and Duration
Although the absolute time (or number) of monitoring events required to characterize long-term attenuation rate depends on the short-term variability and the attenuation rate, the trade-off between monitoring frequency and time is independent of these parameters. If you reduce monitoring frequency (e.g., from quarterly to semi-annual monitoring), then you need to extend the total monitoring time in order to characterize the long-term attenuation rate with the same level of confidence or accuracy. The trade-off between monitoring frequency and time required to characterize the long-term trend is defined by the mathematics of linear regression and is the same at every site[7]. At all sites, five years of semi-annual monitoring data (10 monitoring events total) provides the same information about the long-term attenuation as four years of quarterly monitoring data (16 monitoring events) regardless of the inherent level of event-to-event variability at the site. Thus, switching from quarterly to semi-annual monitoring will reduce the number of monitoring events needed to characterize the long-term trend by 38%, but the amount of time needed will increase by 25%. The trade-off between monitoring frequency and monitoring duration is summarized in Table 2.
Summary
Site managers can use statistical methods and software tools to analyze long-term groundwater monitoring data. These methods and tools can be used to answer key questions about the long-term trends in these data, such as “are the concentrations decreasing?” and “what is the underlying attenuation rate?” Managers should always consider how much data is needed to address these questions as well as the inherent trade-off between monitoring frequency and duration when considering the data collection strategy.
References
- ^ 1.0 1.1 ITRC, 2013. Groundwater statistics and monitoring compliance, statistical tools for the project life cycle. GSMC-1. Washington, D.C.: Interstate Technology & Regulatory Council, Groundwater Statistics and Monitoring Compliance Team. Report pdf
- ^ 2.0 2.1 McHugh, T.E., Kulkarni, P.R., Beckley, L.M., Newell, C.J., Strasters, B., 2015. Methods for minimization and management of variability in long-term groundwater monitoring results. A new method to optimize monitoring frequency and evaluate long-term concentration trends, Technical Report, Task 2 & 3. ER-201209. ER-201209
- ^ Gilbert, R.O., 1987. Statistical methods for environmental pollution monitoring. John Wiley & Sons. ISBN 978-0-471-28878-7
- ^ Singh, A., Maichle, R. and Lee, S.E., 2006. On the computation of a 95% upper confidence limit of the unknown population mean based upon data sets with below detection limit observations. U.S. Environmental Protection Agency, EPA-600-R-06-022. Report pdf
- ^ AFCEC (Air Force Civil Engineer Center), 2012. Monitoring and remediation optimization system (MAROS) software, user's guide and technical manual. In: Air Force Center for Environmental Excellence. MAROS
- ^ Connor, J.A., Farhat, S.K. and Vanderford, M., 2014. GSI Mann‐Kendall toolkit for quantitative analysis of plume concentration trends. Groundwater, 52(6), 819-820. doi: 10.1111/gwat.12277
- ^ 7.0 7.1 McHugh , T.E., Kulkarni, P.R., and Newell, C.J., 2016. Time Vs. Money: A Quantitative Evaluation of Monitoring Frequency Vs. Monitoring Duration. Groundwater, 54, 692–698. doi: 10.1111/gwat.12407